고유값분해는 선형대수학의 핵심 중의 핵심이라고 생각됩니다. 고유값과 고유벡터를 산술적으로 구하는 것은 그렇게 어렵지 않으나, 고유값과 고유벡터가 물리적으로 어떤 의미를 갖는지를 이해하는 것은 조금 난해합니다. 오늘은 제가 이해한 바를 다시 정리해보려고 합니다.
어떤 벡터에 어떤 행렬 A를 곱하면, 행렬 A의 고유값 중에서 가장 큰 고유값과 매칭되는 고유벡터의 방향에 가장 크게 영향을 받습니다. 이것이 무슨 말인지, 예를 통해 설명해보겠습니다.
다음과 같은 벡터가 있다고 가정해봅시다.

이 벡터에 다음과 같은 행렬 A를 곱해주겠습니다.

그러면

가 됩니다.

이 결과가 고유벡터와 무슨 상관이 있는지 살펴보겠습니다. 먼저 행렬 A의 고유값과 고유벡터를 구해보겠습니다. 2x2 행렬이므로 고유값은 비교적 간단히 구할 수 있습니다. 2x2 행렬이므로 고유값은 2개가 존재합니다. 이 고유값의 곱은 이 행렬의 행렬식이 되고, 이 고유값의 합은 이 행렬의 trace가 됩니다. 따라서 다음과 같은 식을 세울 수 있습니다.
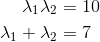
이것을 풀면, 고유값은 5, 2가 나옵니다. 자 그럼 고유값 5에 대응하는 고유벡터를 구해보겠습니다.

위 식을 만족시키는 x1은 여러개가 있지만, 간단하게

을 고유값 5의 고유벡터로 삼겠습니다. 이번에는 고유값 2에 대응하는 고유벡터를 구하겠습니다.

가능한 고유벡터로 아래의 것을 선택하겠습니다.

이제 위 그래프에 고유벡터들을 추가해보겠습니다.
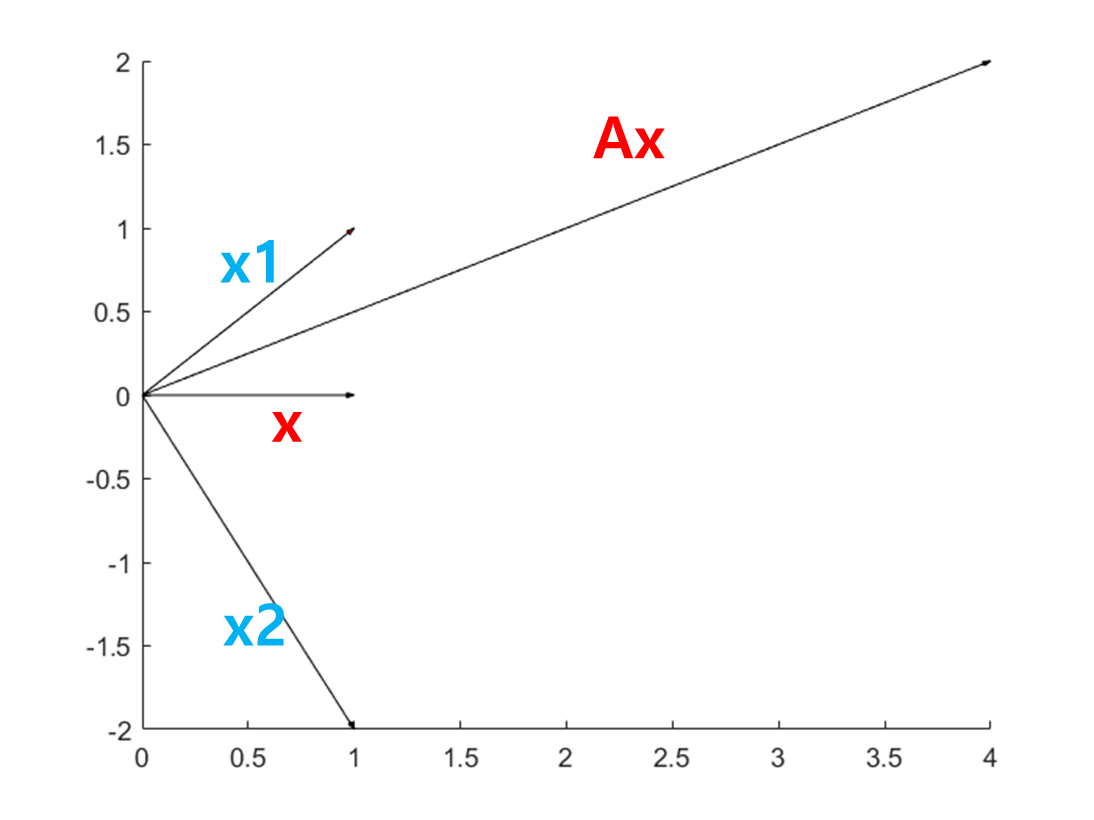
여기서 관찰할 수 있는 것은 Ax의 방향은 큰 고유값과 매칭되어 있는 고유벡터 x1의 방향과 더 가깝다는 것입니다. x1과 x2가 Ax의 방향에 영향을 미치는데 더 큰 고유값과 매칭되어 있는 x1이 더 큰 영향을 미친 것입니다.
이번에는 x가 A의 첫번째 고유벡터와 같은 경우를 보겠습니다.
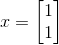
이때 Ax는 다음과 같습니다.
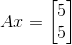
이 경우를 그림으로 살펴보겠습니다.

Ax의 방향은 x 및 x1의 방향과 완전히 같다는 것을 알 수 있습니다. 그리고 크기는 5배죠. 바로 고유값 크기만큼 길어졌습니다. 이래서 $Ax = \lambda x$인 것이죠.
마지막으로 x가 A의 두번째 고유벡터와 같은 경우를 살펴보겠습니다.

이때 Ax는 다음과 같이 계산됩니다.

역시 그림으로 나타내겠습니다.

이 경우에 Ax의 방향은 x 및 x2의 방향과 같고 크기는 고유값인 2배 만큼 큽니다.
따라서 고유값과 고유벡터 물리적 의미를 다음과 같이 결론지을 수 있습니다. 고유벡터는 방향을 결정하고, 고유값은 그 방향으로의 세기를 결정한다.
'Research > 선형대수학' 카테고리의 다른 글
| [bskyvision의 선형대수학, 제2강] 점곱과 길이 (0) | 2021.01.25 |
|---|---|
| [bskyvision의 선형대수학, 제1강] 벡터와 선형결합 (6) | 2021.01.18 |
| [bskyvision의 선형대수학, 제0강] 동기부여: 선형대수학 F 받았던 학생이 선형대수학을 이용해서 SCI 논문을 쓰다 (8) | 2021.01.13 |
| [선형대수학] 놈(norm)이란 무엇인가? (13) | 2020.06.25 |
| [선형대수학] 헤시안(Hessian) 행렬과 극소점, 극대점, 안장점 (12) | 2019.12.11 |
| [선형대수학] 가우스-요르단 소거법으로 n차 정방행렬의 역행렬 구하기 (0) | 2019.06.25 |
| [선형대수학] 두 행렬의 곱을 바라보는 세 가지 관점 (6) | 2019.06.24 |
| [선형대수학] 행렬A의 행사다리꼴 및 기약행사다리꼴 (0) | 2018.01.16 |