이산 확률 분포 정리(균일분포, 이항분포, 포아송분포)
최근에 S금융그룹의 한 자회사에서 면접을 봤습니다. 면접관 중 한 분께서 이산 확률 분포 중에 아는 것들을 말해보라고 하셨습니다. 너무 오래 전에 수학한 내용이라 기억나지 않았는데, 균일 분포라는 단어 하나가 생각 나서 "uniform distribution도 이산 확률 분포 아닌가요?"라고 말씀 드렸습니다. 면접관님이 친절하게 이산 확률 분포에는 대표적으로 이항분포와 포아송분포가 있다고 말씀을 해주시더라고요.
'아! 그런 게 있었지... 반갑다... 그런데 이게 어떤 의미를 지니는지 모르겠다...'
역시 사람은 망각의 동물입니다. ㅋㅋ 언제 또 어떤 모습으로 다시 만나게 될 지 모르는 개념들이기 때문에 다시금 정리하면서 머리에 새겨보려고 합니다.
이산 확률 분포
우선 이산 확률 분포를 논하기 전에 확률 분포라는 것을 먼저 다뤄야 할 것 같습니다. 확률 분포(probability distribution)는 확률 변수가 어떤 값이 나올 확률들의 분포를 의미합니다. 또 확률 변수라는 단어를 먼저 살펴봐야겠네요.
확률 변수라는 것은 취할 수 있는 값이 확률에 의해 정의되어 있는 변수를 뜻합니다. 예를 들어, 주사위를 던질 때 1, 2, 3, 4, 5, 6이 나올 확률은 각각 1/6으로 정해져 있습니다. 이렇게 나올 수 있는 결과가 유한히 정해져 있는 확률 변수를 이산 확률 변수라고 부릅니다. 반면, 제주도 어느 귤 밭에서 수확한 귤의 무게는 50.0g, 51.2g, 49.3g, 49.4g 등으로 무한할 것입니다. 이러한 확률 변수는 연속 확률 변수라고 부릅니다.
이 글에서는 이산 확률 변수가 취할 수 있는 값과 그 값이 나올 확률의 관계를 나타내는 이산 확률 분포에 대해서만 다루도록 하겠습니다. 이산 확률 분포에는 균일 분포, 이항 분포, 포아송 분포 등이 있습니다.
균일 분포
방금 예시로 든 주사위 한 개를 던져서 각 눈이 나올 확률은 모두 1/6로 균일합니다. 이러한 확률 분포를 균일 분포(uniform distribution)라고 부릅니다.

이항 분포
동전을 5번 던져서 2번 앞면이 나올 확률은 얼마일까요? 이렇게 두 가지 경우의 수밖에 없는 시행을 반복할 때 나올 수 있는 값의 확률 분포를 나타내는 것이 이항 분포(binomial distribution)입니다.
동전을 5번 던졌을 때 0번 앞면이 나올 확률은 다음과 같습니다.
(5번 중 0번 앞면이 나오는 조합의 수) * (0.5)^0 * (0.5)^5 =
5C0 * (0.5)^0 * (0.5)^5 = 1 * (0.5)^0 * (0.5)^5 = 0.031
동전을 5번 던졌을 때 1번 앞면이 나올 확률:
(5번 중 1번 앞면이 나오는 조합의 수) * (0.5)^1 * (0.5)^4 =
5C1 * (0.5)^1 * (0.5)^4 = 5 * (0.5)^1 * (0.5)^4 = 0.156
동전을 5번 던졌을 때 2번 앞면이 나올 확률:
(5번 중 2번 앞면이 나오는 조합의 수) * (0.5)^2 * (0.5)^3 =
5C2 * (0.5)^2 * (0.5)^3 = 10 * (0.5)^2 * (0.5)^3 = 0.313
동전을 5번 던졌을 때 3번 앞면이 나올 확률:
(5번 중 3번 앞면이 나오는 조합의 수) * (0.5)^3 * (0.5)^2 =
5C3 * (0.5)^3 * (0.5)^2 = 10 * (0.5)^2 * (0.5)^3 = 0.313
동전을 5번 던졌을 때 4번 앞면이 나올 확률:
(5번 중 4번 앞면이 나오는 조합의 수) * (0.5)^4 * (0.5)^1 =
5C4 * (0.5)^4 * (0.5)^1 = 5 * (0.5)^4 * (0.5)^1 = 0.156
동전을 5번 던졌을 때 5번 앞면이 나올 확률:
(5번 중 5번 앞면이 나오는 조합의 수) * (0.5)^5 * (0.5)^0 =
5C5 * (0.5)^5 * (0.5)^0 = 1 * (0.5)^5 * (0.5)^0 = 0.031
이 확률 변수의 값에 대한 확률들을 막대 그래프로 나타내면 이항 분포 그래프가 그려집니다. 동전을 5번 던지면 앞면이 2번이나 3번 나올 확률이 가장 높다는 것을 알 수 있습니다.
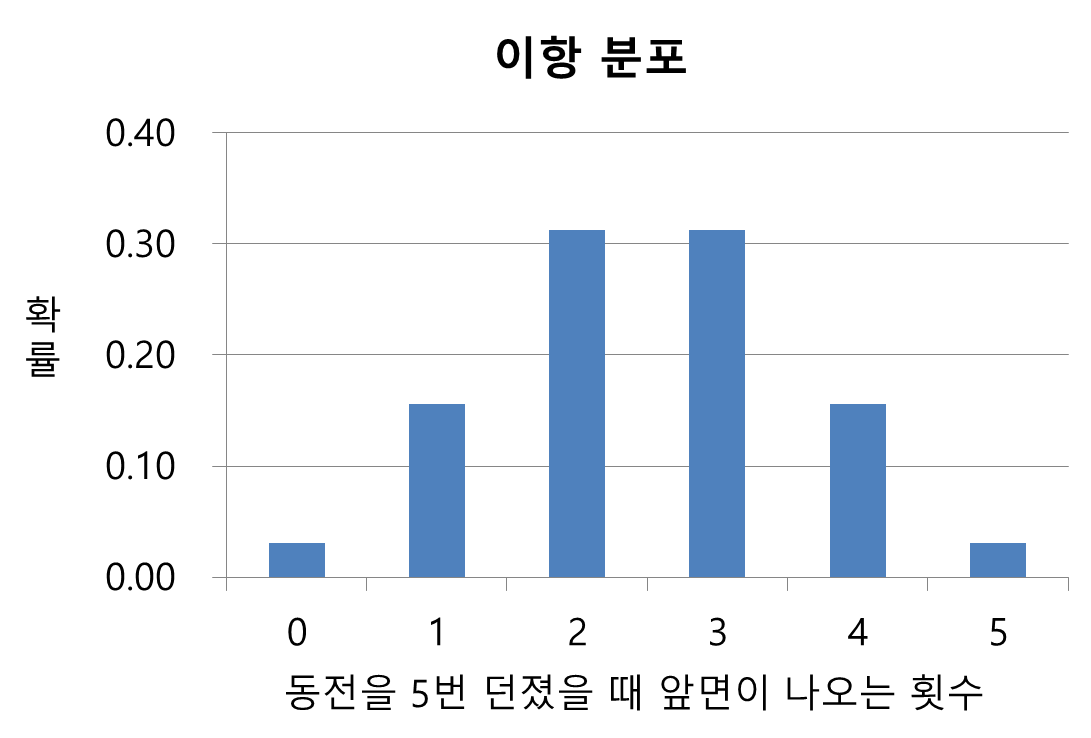
만약 친구와 동전 5번 던졌을 때 앞면이 나올 횟수를 맞히는 것으로 내기를 했다면, 2 또는 3에 걸어야겠죠. 만약 동전 5번 던졌을 때 앞면이 나올 횟수에 배당률을 산정한다면, 2, 3에 가장 적은 배당률을 책정해야 할 것이고, 0, 5에 가장 큰 배당률을 줘야 할 것입니다.
포아송 분포
어떤 결과가 발생할 확률은 아주 작고 시행의 횟수는 클 때의 확률 분포는 포아송 분포를 따릅니다. 식으로는 다음과 같이 나타낼 수 있습니다.
$f(x) = \frac{e^{-\lambda}\lambda^x}{x!}$
불량품이 만들어진 확률이 0.2%인 어떤 공장에서 1000개의 제품을 생산하면 평균적으로 불량품이 2개 만들어질 것입니다. $\lambda = 2$인 경우입니다. 이 경우의 포아송 분포의 식은 다음과 같습니다.
$f(x) = \frac{e^{-2}2^x}{x!}$
이 상황에서 0개의 불량품이 만들어질 확률은 $f(0) = \frac{e^{-2}2^0}{0!} = 0.135$입니다.
1개의 불량품이 만들어질 확률:
$f(1) = \frac{e^{-2}2^1}{1!} = 0.271$
2개의 불량품이 만들어질 확률:
$f(2) = \frac{e^{-2}2^2}{2!} = 0.271$
3개의 불량품이 만들어질 확률:
$f(3) = \frac{e^{-2}2^3}{3!} = 0.180$
그렇다면, 이 공장에서 1000개의 제품을 생산할 때 불량품이 3개 이하일 확률은 f(0) + f(1) + f(2) + f(3) = 0.857로 85.7%가 될 것입니다. 이 분포를 그래프로 그리면 다음과 같습니다.
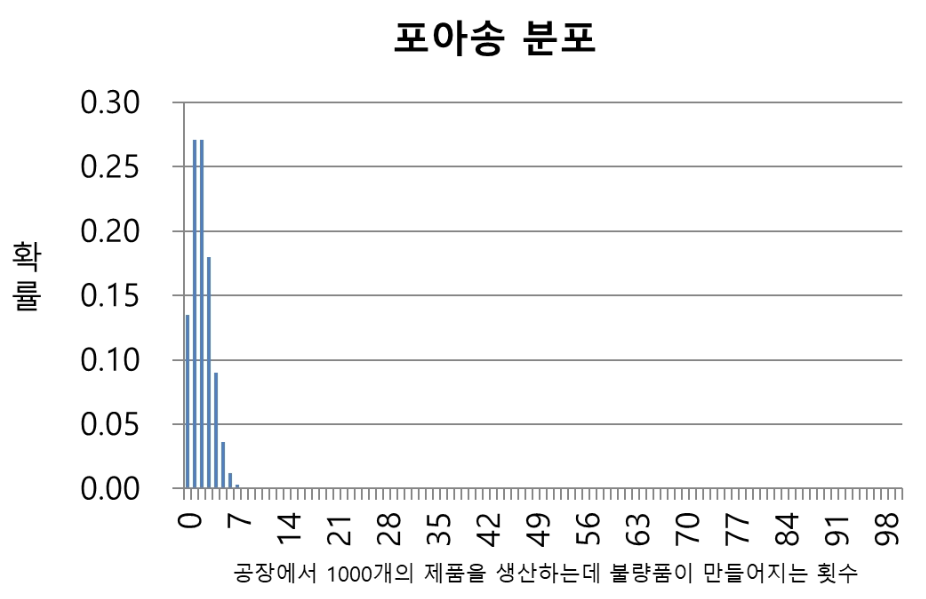
이 회사의 사장 또는 이 회자의 투자자는 이렇게 명령을 내릴 수도 있을 것입니다.
"공정율을 높여서 1000개 제품 생산시 3개 이하의 불량품이 만들어질 확률을 90%로 높이세요!"
관련 글
참고자료
[1] 쿠리하라 신이치, 마루야마 아츠시 지음, "통계학 도감", 성안당(2018)