Harris 코너 검출기의 이해
디지털 이미지는 점들, 즉 픽셀들의 집합으로 구성되어 있습니다. 그 점들 중에서 가장 중요한 점들은 단연 코너점들입니다. 코너점(corner point)이란 두 방향 이상에서 변화가 급격한 점입니다. 반면 엣지점(edge point)은 한 방향에서 변화가 급격한 점입니다. 이도 저도 아닌 점들은 평탄한 점(flat point)이라고 부릅니다.
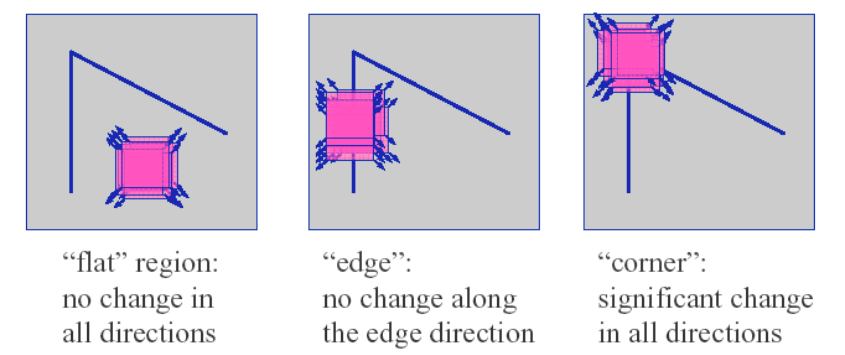
코너점이 중요한 이유는 이미지에서 가장 중요한 구조 정보를 담고 있기 때문입니다. 다른 정보를 모두 없애고 코너점들만 남겨놔도 이미지 내의 물체들의 형상을 대충 알 수 있습니다.
그러면 오늘은 가장 기초적이면서도 효율적인 코너점 검출기인 Harris 코너 검출기에 대해서 알아보겠습니다. Harris 코너 검출기는 1988년에 Harris와 Stephens에 의해 작성된 논문 "A combined corner and edge detector"에서 소개된 방법입니다. 제가 태어난 해에 나온 방법이니 벌써 32살이 된 방법이네요. ㅎㅎ
Harris 코너 검출기의 기본 원리는 다음과 같습니다.
한 픽셀을 중심에 놓고 작은 윈도우(window)를 설정한 후에, 이 윈도우를 x축 방향으로 u만큼, y축 방향으로 v만큼 이동시킵니다.

그 다음 윈도우 내의 픽셀 값들의 차이의 제곱의 합을 구해줍니다.
$E(u, v) = \sum _{(x_k, y_k)\in W} [I(x_k+u, y_k+v)-I(x_k,y_k)]^2$
한 마디로 얼마나 변화했는지를 계산해주는 것입니다. 코너점이라면 x축, y축 방향 모두 많이 변화했겠지요? 따라서, 이 E값이 크면 코너점이라고 보는 것입니다.
그런데, 이 식은 테일러 확장에 의해 다음과 같이 근사됩니다.
$\begin{align*}
E(u, v) &= \sum _{(x_k, y_k)\in W} [I(x_k+u, y_k+v)-I(x_k,y_k)]^2
\\
&\approx \sum _{(x_k, y_k)\in W}(\frac{\partial I}{\partial x}u)^2 + (\frac{\partial I}{\partial y}v)^2 + 2\frac{\partial I}{\partial x}\frac{\partial I}{\partial y}uv
\end{align*}$
그리고 이것을 행렬로 나타내면, 다음과 같이 됩니다.
$E(u, v) = \begin{bmatrix}
u & v
\end{bmatrix}
\begin{bmatrix}
\sum (\frac{\partial I}{\partial x})^2 & \sum \frac{\partial I}{\partial x}\frac{\partial I}{\partial y}\\
\sum \frac{\partial I}{\partial x}\frac{\partial I}{\partial y} & \sum (\frac{\partial I}{\partial y})^2
\end{bmatrix}
\begin{bmatrix}
u\\
v
\end{bmatrix}$
E값이 크면 코너점이라고 했는데, E값이 크려면 중간에 위치한 2 x 2행렬의 값이 커야 합니다. 이 행렬을 M이라고 하겠습니다. (이 행렬을 structure tensor라고 부르기도 합니다.)
이 행렬 M을 고유값 분해하면 2개의 고유값과 그에 상응하는 고유벡터들을 얻을 수 있습니다. 두 개 고유값 중에 더 큰 고유값과 연결된 고유벡터 방향으로 이미지의 변화가 가장 큽니다. 반면 작은 고유값과 연결된 고유벡터 방향으로의 이미지 변화는 작습니다. 따라서 만약 두 방향으로 변화가 크면(코너점이면), M의 고유값들은 충분히 큰 값들을 갖습니다. 하나의 고유값은 크고 다른 고유값은 작다면 엣지입니다. 둘 다 0에 가까운 값을 가지면 flat 입니다.
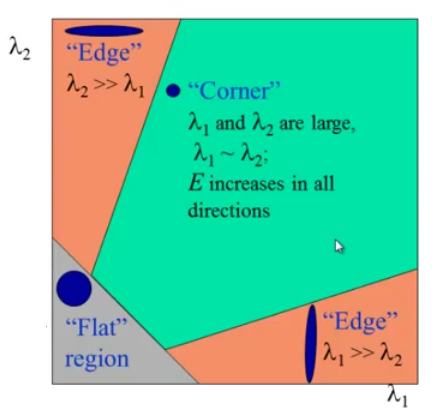
그런데 고유값을 계산하는 것은 계산적으로 복잡한 일이기 때문에, 다음과 같은 공식으로 대체해서 코너인지, 엣지인지, flat인지를 판정해줍니다.
$R = det(M) - k(trace(M))^2$
두 고유값이 모두 크면, R은 0보다 크게 되고, 한 고유값은 크고 다른 한 고유값은 작으면 0보다 작게 되고, 둘다 작으면 0에 가까운 값이 산출됩니다. 따라서, R이 0보다 크면 코너이고, R의 절대값이 0에 가까우면 flat이고, 0보다 작으면 엣지가 되는 것이죠.
그럼 한번 Harris 코너 검출기로 코너점들을 검출해보도록 하겠습니다. Matlab의 Computer vision system toolbox 내에 Harris 코너 검출에 관한 함수, detectHarrisFeatures가 있습니다. 간단한 예로 체스판 이미지에서 코너점들을 찾아보겠습니다.
clc, clear, close all
I= checkerboard;
corners = detectHarrisFeatures(I);
imshow(I);
hold on;
plot(corners.selectStrongest(50));
결과 이미지는 다음과 같습니다.

코너점들을 잘 검출해낸 것을 확인할 수 있습니다. 초록색 마커로 표시되었죠?
예전에 포스팅한 SIFT도 코너점 검출기입니다. Harris 코너 검출기에 비하면 고성능의 코너 검출기죠. SIFT에 관해서는 https://bskyvision.com/21을 참고하세요. bskyvision.com의 아주 초기 포스팅인데, 가장 많이 사랑을 받은 글 중 하나입니다.^^
<참고자료>
[1] https://en.wikipedia.org/wiki/Harris_Corner_Detector, 위키피디아(영문), Harris Corner Detector
[2] https://docs.opencv.org/master/dc/d0d/tutorial_py_features_harris.html, OpenCV, "Harris Corner Detection"
[3] https://stackoverflow.com/questions/23171991/what-does-eigen-value-of-structure-tensor-matrix-denote, Stack Overflow, "What does eigen value of structure tensor matrix denote?"
[4] https://en.wikipedia.org/wiki/Corner_detection#The_Harris_&_Stephens_/_Plessey_/_Shi%E2%80%93Tomasi_corner_detection_algorithms, 위키피디아(영문), Corner detection
[5] https://guangchun.wordpress.com/2013/02/16/harris-detector/, GUANGCHUN, "Understanding Harris corner detector"