[CNN 알고리즘들] SENet의 구조
LeNet-5 => https://bskyvision.com/418
AlexNet => https://bskyvision.com/421
VGG-F, VGG-M, VGG-S => https://bskyvision.com/420
VGG-16, VGG-19 => https://bskyvision.com/504
GoogLeNet(inception v1) => https://bskyvision.com/539
ResNet => https://bskyvision.com/644
SENet => https://bskyvision.com/640
-----
오랜만에 CNN 알고리즘에 대한 글을 쓰네요. 오늘은 SENet 차례입니다. SENet은 2017년 이미지넷 대회에서 우승을 차지한 모델입니다. top-5 error가 2.251%밖에 되지 않습니다. ground-truth인 사람의 top-5 error가 5%라고 하니 대단한 결과죠. 사람보다 이 데이터셋에서만큼은 더 이미지 분류를 잘 해낸다는 뜻입니다.
SENet의 original 논문은 2018년 CVPR에서 발표된 "Squeeze-and-Excitation Networks"입니다. 한국어로 번역해보면 짜내고(squeeze) 활성화시키는(excitatation) 망이라고 볼 수 있습니다. 야구에서 보통 스퀴즈라고 하면 점수를 어떻게든 "짜내기" 위해 희생번트를 대는 등의 전술을 의미하죠? 이것과 SENet의 Squeeze와는 큰 관련은 없지만, Squeeze의 의미는 알게 되셨을 것이라고 생각합니다.
그러면 이제 SENet에 대한 이야기를 시작하도록 하겠습니다. SENet 논문은 기존 어떤 모델에도 적용될 수 있는 SE block이라는 것을 제안했습니다. VGGNet, GoogLeNet, ResNet 등에 SE block을 첨가함으로써 성능 향상을 도모한 것입니다. 성능은 꽤 많이 향상되는 반면, hyperparameter는 많이 늘지 않기 때문에, 연산량 증가는 크지 않습니다. 보통 성능 향상을 시키려면 연산량도 그만큼 엄청나게 증가되는데, SENet의 경우 연산량은 크게 늘지 않으면서도 분류 정확도를 높일 수 있기 때문에 SE block을 사용하는 것은 효율적이라고 볼 수 있습니다.
SE block

그러면, 위 그림을 보면서 SE block에 대해서 설명하겠습니다. X는 특성맵이고 U도 특성맵입니다. $F_{tr}$은 컨볼루션으로 보시면 됩니다. H'xW'xC' 크기의 특성맵 X가 $F_{tr}$ 컨볼루션을 통해 HxWxC 크기의 특성맵 U가 됩니다.
그 다음에 스퀴즈(squeeze)를 실행해줍니다. C개 채널의 2차원(HxW)의 특성맵들을 1x1 사이즈의 특성맵으로 변환해주는 것입니다. 간단히 global average pooling (GAP)을 통해 각 2차원의 특성맵을 평균내어 하나의 값을 얻습니다.
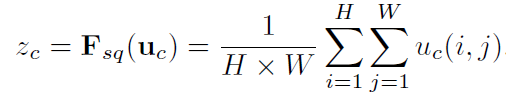
이로인해 각 채널을 하나의 숫자로 묘사할 수 있게 됩니다. 총 C개 채널의 특성맵이 있으므로 1x1xC의 특성맵으로 스퀴즈됩니다. 특성맵을 global하게 표현한 것이죠. 컨볼루션이 local 정보를 다룬다면, 스퀴즈는 global 정보를 다룬다고 볼 수 있습니다.
스퀴즈 후에는 활성화(excitation) 작업에 돌입합니다. 두 개의 Fully-connected(FC) 층을 더해줘서 각 채널의 상대적 중요도를 알아내는 겁니다.
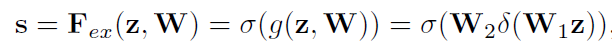
$\sigma$는 시그모이드함수이고, $\delta$는 ReLU 함수입니다. 위 공식을 살펴보자면, 먼저 스퀴즈를 통해 얻은 $z_c$을 인풋으로 삼아서 $W_1$ 가중치들과 fully-connected하게 곱해줍니다. 그래서 얻은 값을 $\delta$, 즉 ReLU 함수로 활성화해준 후에 $W_2$ 가중치들과 fully-connected하게 곱해줍니다. 그렇게 얻은 값을 $\sigma$, 즉 시그모이드 함수로 활성화해줘서 0과 1사이의 값을 갖게 합니다. 따라서 각 채널의 상대적 중요도를 0과 1의 값으로 파악할 수 있게 됩니다.
여기서 기억해야할 것은 FC 층들이 병목(bottle-neck) 구조가 되게 만든다는 것입니다. 은닉(hidden) 층의 뉴런의 갯수를 입력 층보다 작게 해줍니다. 그리고 출력 층의 뉴런의 갯수는 입력 층과 동일하게 해줍니다. 병목 구조로 해주는 이유는 hyper-parameter의 갯수를 많이 늘리지 않기 위함도 있고, 일반화에 도움을 주기 위함도 있습니다. 은닉 층의 뉴런 갯수는 reduction ratio, r값에 의해 결정됩니다. r이 클수록 은닉 층의 뉴런 갯수가 더 적어지고, 복잡도도 더 낮아집니다. 따라서 각 층의 뉴런의 갯수는 채널의 갯수인 C에서 시작해서 C/r로 감소했다가 다시 C로 증가합니다.
이렇게 얻은 C개의 $s_c$를 $u_c$에 각각 곱해줘서 U를 재보정해줍니다. 그것을 $\tilde{X}$라고 합니다.
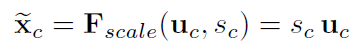
정리하자면, 특성맵은 X에서 컨볼루션을 통해 U로, U에서 SE block을 통해 $\tilde{X}$로 변환됩니다.
SE block의 목적은 한마디로 컨볼루션을 통해 생성된 특성을 채널당 중요도를 고려해서 재보정(recalibration)하는 것입니다. 이러한 SE block을 컨볼루션 연산 뒤에 붙여줌으로써 성능 향상을 도모한 것이 바로 SENet의 핵심입니다.
기존 CNN 모델과의 결합
위에서 말씀드린대로 SE block은 기존의 CNN 모델들에 붙여서 사용할 수 있습니다. VGGNet의 경우에는 컨볼루션 및 활성화 뒤에 바로 붙이면 되고, GoogLeNet의 경우에는 Inception 모듈 뒤에 붙이면 되고, ResNet의 경우에는 Residual 모듈 뒤에 붙이면 됩니다. 다음과 같이 말이죠.
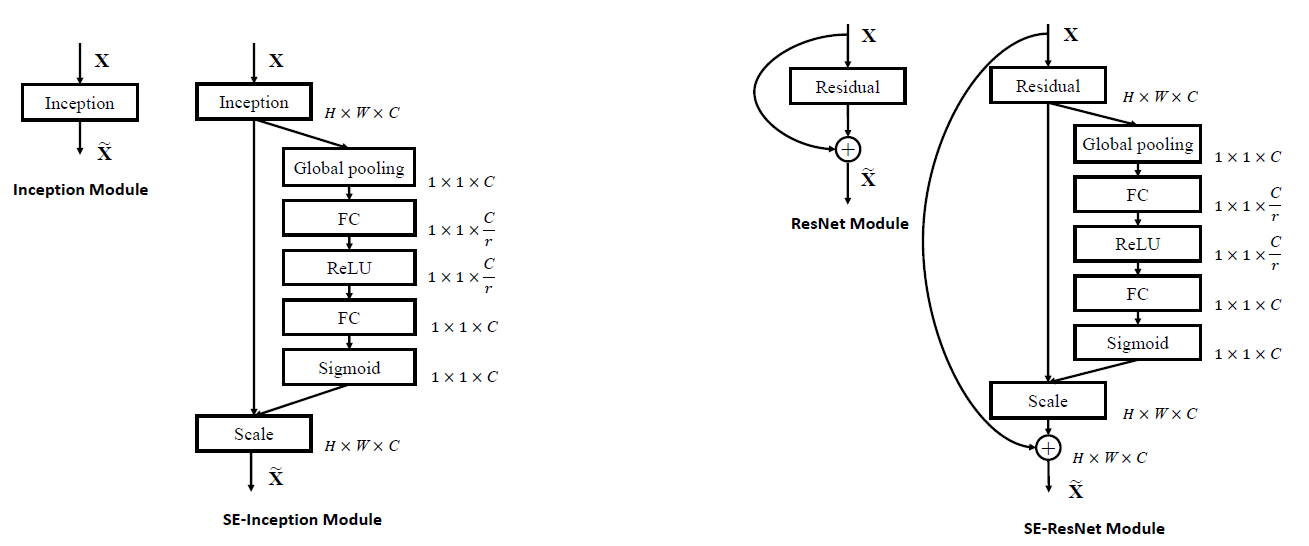
GoogLeNet과 ResNet에 대한 이전 글들을 읽으신 분들은 이 그림만으로도 SE block을 어떻게 덧붙이는지 이해가 되실 것이라고 생각합니다.
성능 분석
SENet 논문에 성능에 관한 여러 표들이 있지만 가장 중요한 두 개의 표만 보여드리겠습니다. 너무 많은 표를 보여드리면 오히려 이해하는데 방해가 될 수도 있을 것 같아서입니다.

위 표에서 original은 original 논문에서 얻은 결과를, re-implementation은 저자들이 직접 실험해서 얻은 결과를, SENet은 SE block을 첨가해서 얻은 결과를 각각 나타냅니다. 이 표를 통해 알 수 있는 것은 SE block을 첨가했을 때 항상 top-1 error와 top-5 error를 낮췄다는 것입니다. 그리고 알고리즘의 복잡도는 크게 증가하지 않았다는 것도 GFLOPs 열에서 알 수 있습니다.
SENet이 출시된 당시 최신 알고리즘들과 이미지넷에서의 성능을 비교한 표는 다음과 같습니다. SENet-154는 SE block을 개정된 ResNeXt와 통합한 것을 의미합니다. ResNeXt에 관한 논문은 아직 안 읽어봤습니다.^^; 이름으로 유추할 수 있는 것은 ResNet을 좀 더 발전시킨 모델 같습니다. 아무튼, SENet-154가 그당시 최신 모델들보다 우월한 성능을 보임을 아래 표를 통해 알 수 있습니다.

이것으로 SENet에 관한 설명은 마치려고 합니다. Squeeze와 Excitation이라는 어찌보면 간단한 과정을 통해 성능을 이렇게 향상시킬 수 있다는 것이 놀랍습니다. 저자들은 이런 걸 어떻게 생각해냈을까 싶기도 하고... ㅎㅎ 수많은 노력과 시행착오와 행운의 결과겠죠? 저도 SENet과 같이 학계에 큰 영향력을 줄 수 있는 모델 하나 개발해보고 싶네요.
아마 당분간 이미지 분류용 CNN 알고리즘에 대한 글은 작성하지 않을 것 같습니다. SENet보다 확실히 우월한 모델이 나오지 않는 한 말이죠. 대신 물체 검출(object detection), 의미적 분할(semantic segmentation) 등 다른 컴퓨터 비전 과제를 위한 CNN 알고리즘에 대한 글을 작성해보려고 합니다. 도움이 될만한 글을 작성하도록 노력하겠습니다. 항상 질문과 지적은 환영합니다. 빠르게 답변하도록 노력하고 있으니 댓글 남겨주세요.^^
<참고자료>
[1] https://jayhey.github.io/deep%20learning/2018/07/18/SENet/, Jaeyun's Blog, "SENet(Squeeze and exitation networks)"
[2] https://wwiiiii.tistory.com/entry/SqueezeandExcitation-Networks, 기리이이이인, "Squeeze-and-Exitation Networks"