LeNet-5 => https://bskyvision.com/418
AlexNet => https://bskyvision.com/421
VGG-F, VGG-M, VGG-S => https://bskyvision.com/420
VGG-16, VGG-19 => https://bskyvision.com/504
GoogLeNet(inception v1) => https://bskyvision.com/539
ResNet => https://bskyvision.com/644
SENet => https://bskyvision.com/640
-----
컨볼루션 신경망(CNN)은 딥러닝 알고리즘 중에 컴퓨터 비전 분야에서 절대 강자로 군림하고 있다. CNN 알고리즘 중 LeNet-5와 AlexNet에 대해서는 이미 소개했다.
옥스포드 대학의 연구팀 VGG에 의해 개발된 VGGNet은 2014년 이미지넷 이미지 인식 대회(ILSVRC)에서 준우승했다. 준우승한 모델이긴 하지만 오히려 우승한 모델인 GoogLeNet보다 더 각광받았다. 이 VGGNet부터 네트워크의 깊이가 확 깊어지기 시작했다. 여기서 말하는 VGGNet은 VGG16, VGG19와 같은 모델들이다.
그러나 옥스포드 대학의 VGG팀은 VGG16, VGG19를 개발하기 전에, 먼저 AlexNet과 거의 유사한 CNN 모델들을 개발했었다. VGG-F, VGG-M, VGG-S로 불리는 모델들이다. 오늘은 바로 그 모델들에 대해서 정리하고자 한다. VGG16, VGG19에 대해서는 머지 않은 시일 내에 포스팅할 것이다.
VGG-F, VGG-M, VGG-S 모델을 담고 있는 original 논문의 제목은 "Return of the Devil in the Details: Delving Deep into Convolutional Nets"이다. 2014년에 게재되었다.
VGG-F, VGG-M, VGG-S의 구조
VGG-F, VGG-M, VGG-S는 속도와 정확도의 트레이드오프를 고려한 모델들이다. VGG-F는 fast, 즉 빠름에 초점을 맞춘 모델이고, VGG-S는 slow, 즉 느리지만 정확도에 초점을 맞춘 모델이다. VGG-M은 medium으로 이 둘의 중간 정도라고 보면 된다. VGG-F, VGG-M, VGG-S의 세부적 내용은 다음 표에서 잘 설명하고 있다.

VGG-F, VGG-M, VGG-S는 표에서 알 수 있듯이 5층의 컨볼루션 층들과 3층의 fully-connected 층들로 구성되어 있다. 이 글에서는 VGG-F를 중점으로 설명하려고 한다. VGG-F에 대한 설명을 잘 읽고나면 VGG-M과 VGG-S도 충분히 이해할 수 있을 것이라 생각한다.
0) 인풋: VGG-F는 224 x 224 x 3 사이즈의 이미지(224 x 224의 RGB 컬러이미지)를 입력받을 수 있다.
1) 첫번째 레이어(컨볼루션 레이어, conv1): 64개의 11 x 11 x 3 사이즈 필터커널로 입력영상을 컨볼루션해준다. 이때 컨볼루션의 보폭(stride)은 4로 설정해주고, zero-padding은 사용하지 않는다. zero-padding이란 컨볼루션시 영상의 가장자리 부분에 0을 추가하여 가장자리에 있는 정보의 손실을 줄이는 것이다. 결과적으로 54 x 54 사이즈의 64장의 특성맵이 산출된다. 컨볼루션으로 산출되는 특성맵의 크기를 계산하는 방법과 관련해서는 아래 따로 설명해놓았다. ReLU 활성화 함수로 특성맵은 활성화된다. 그 다음에는 LRN(local response normalization)을 시행한다. 그 다음에 최대 풀링(max pooling)을 적용하여 2만큼 다운샘플링(downsampling)해준다. 그 결과 64장의 특성맵의 사이즈가 27 x 27로 줄어든다. 참고로 ReLU 활성화 함수 및 LRN에 대한 설명은 AlexNet 포스팅에서 찾아볼 수 있다.
2) 두번째 레이어(컨볼루션 레이어, conv2): 256개의 5 x 5 x 64 사이즈 필터커널로 특성맵을 컨볼루션해준다. (전 층에서 생성된 64장의 특성맵을 입체적으로 겹쳐놓고 5 x 5 x 64 사이즈의 3차원 입체 필터커널로 컨볼루션해준다는 뜻이다.) 컨볼루션 보폭은 1로 설정하고, zero-padding은 2만큼 해준다. 결과적으로 27 x 27 사이즈의 256장의 특성맵이 산출된다. 역시 ReLU 활성화 함수를 적용한 후, LRN을 적용한다. 그 다음에 최대 풀링을 이용해서 2만큼 다운샘플링 해준다. 따라서 256장의 27 x 27 사이즈의 특성맵이 13 x 13으로 작아진다.
3) 세번째 레이어(컨볼루션 레이어, conv3): 256개의 3 x 3 x 256 사이즈 필터커널로 특성맵을 컨볼루션해준다. 컨볼루션 보폭은 1로 설정하고, zero-padding은 1만큼 해준다. 결과적으로 13 x 13 사이즈의 256장의 특성맵이 산출된다. ReLU활성화 함수를 적용한다.
4) 네번째 레이어(컨볼루션 레이어, conv4): 256개의 3 x 3 x 256 사이즈 필터커널로 특성맵을 컨볼루션해준다. 컨볼루션 보폭은 1로 설정하고, zero-padding은 1만큼 해준다. 결과적으로 13 x 13 사이즈의 256장의 특성맵이 산출된다. ReLU활성화 함수를 적용한다.
5) 다섯번째 레이어(컨볼루션 레이어, conv5): 256개의 3 x 3 x 256 사이즈 필터커널로 특성맵을 컨볼루션해준다. 컨볼루션 보폭은 1로 설정하고, zero-padding은 1만큼 해준다. 결과적으로 13 x 13 사이즈의 256장의 특성맵이 산출된다. ReLU활성화 함수를 적용한다. 그 다음에 최대 풀링을 이용해서 2만큼 다운샘플링 해준다. 256장의 13 x 13 사이즈의 특성맵이 6 x 6으로 작아진다.
6) 여섯번째 레이어(fully-connected 레이어, full6): 전 층에서 생성된 6 x 6 x 256의 특성맵을 flatten 해준다. flatten이란 전 층의 아웃풋을 1차원의 벡터로 펼쳐주는 것을 의미한다. 따라서 6 x 6 x 256 = 9216개의 뉴런이 되고 full6층의 4096개 뉴런과 fully connected된다. 4096개의 뉴런으로 출력된 것을 ReLU 함수로 활성화해준다. 과적합을 막기 위해 full6에는 훈련시 dropout이 적용된다. dropout에 대해서는 AlexNet 포스팅을 참고하자.
7) 일곱번째 레이어(fully-connected 레이어, full7): 4096개의 뉴런으로 구성되어 있다. full6의 4096개 뉴런과 fully-connected(전 층과 이번 층의 모든 뉴런이 서로 다 연결)되어 있다. 출력된 값을 역시 ReLU 함수로 활성화해준다. full7에는 훈련시 dropout이 적용된다.
8) 여덟번째 레이어(fully-connected 레이어, full8): 1000개의 뉴런으로 구성되어 있다. full7의 4096개 뉴런과 fully-connected 되어 있다. 출력된 값은 softmax 함수로 활성화되어 입력된 이미지가 어느 클래스에 속하는지 알 수 있게 해준다.
왜 VGG-F가 가장 빠른가?
방금 전 챕터에서 VGG-F의 구조에 대해서 자세히 살펴봤다. 글의 초반부에 VGG-F가 VGG-M과 VGG-S에 비해 계산에 있어 더 빠르다고 했는데, 그 이유에 대해 살펴보려고 한다.
먼저 VGG-F와 VGG-M의 연산량을 비교해보자. 연산량에 가장 큰 차이를 유발하는 곳은 바로 첫번째 레이어다. VGG-F는 첫번째 레이어에서 입력영상을 64개의 11 x 11 x 3 사이즈 필터커널로 보폭 4로 컨볼루션해주는 반면, VGG-M은 첫번째 레이어에서 입력영상을 96개의 7 x 7 x 3 사이즈 필터커널로 보폭 2로 컨볼루션해준다. 필터커널의 사이즈가 작을수록, 또한 보폭이 작을수록 연산량은 많아진다.
이번에는 VGG-M과 VGG-S의 연산량을 비교해보자. 연산량에 가장 큰 차이를 유발하는 곳은 바로 두번째 레이어다. 두번째 레이어에서 VGG-S는 VGG-M이 보폭2로 컨볼루션을 진행하는 것과 달리 보폭1로 컨볼루션을 진행한다.
이와 같은 이유로 VGG-F가 VGG-M보다 빠르고, VGG-M은 VGG-S보다 빠르다. 반면 느린 만큼 정확도는 VGG-S가 가장 좋다.
특성맵 크기 계산 관련
컨볼루션 이후 산출되는 특성맵의 크기 계산해서 좀 더 설명할 필요가 있어보인다. 간단한 예를 들어 실제로 특성맵의 크기를 구해보자. 9 x 9 사이즈의 입력 영상을 zero padding을 1만큼 해준 후 5 x 5 사이즈의 필터커널로 컨볼루션을 해주면 산출되는 특성맵의 크기는 어떻게 될까? 컨볼루션 보폭(stride)은 1로 설정하겠다.
zero padding이 1만큼 이뤄진 후에는 다음과 같이 11 x 11 사이즈의 이미지가 된다.
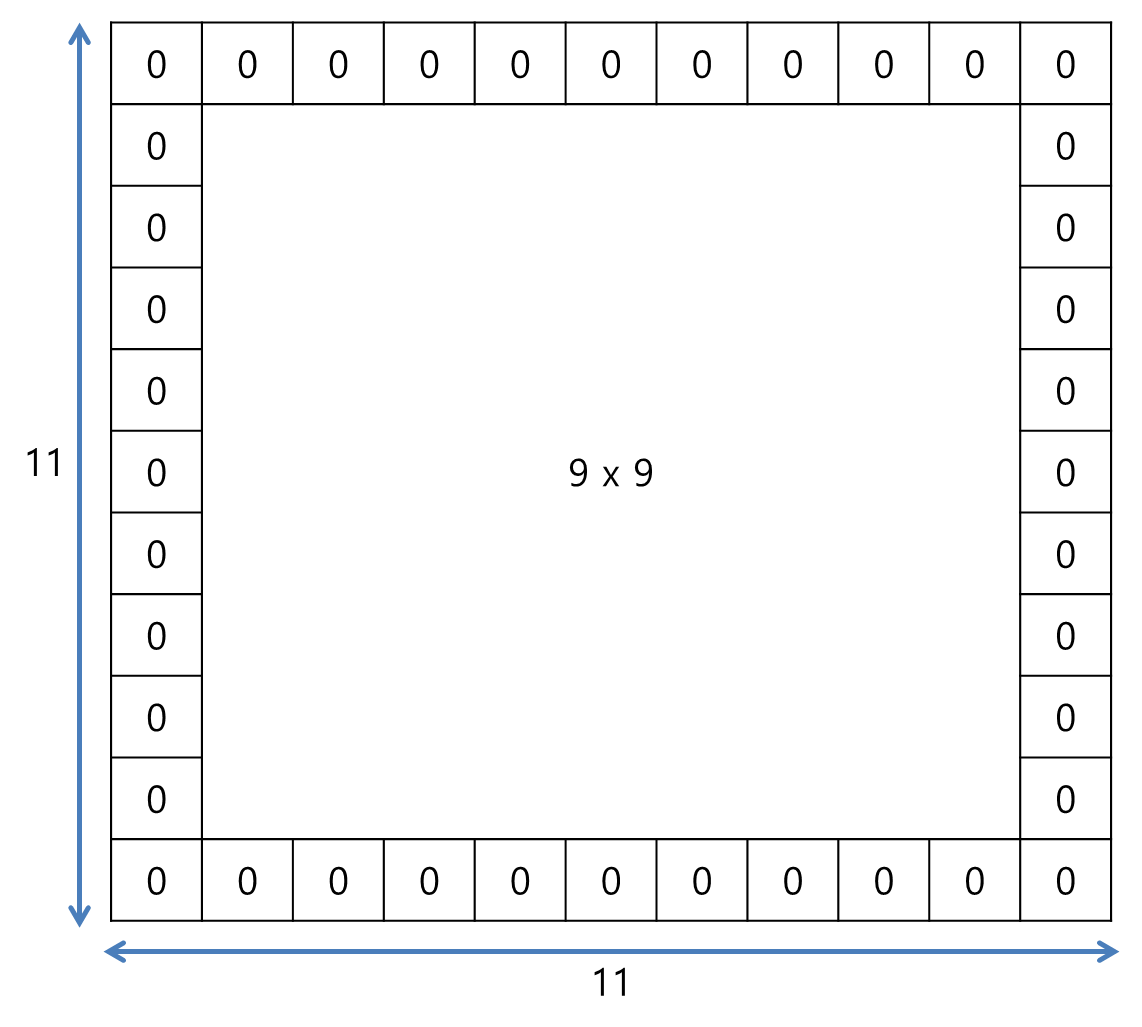
가장자리에 0이 하나씩 더 추가된 것을 확인할 수 있을 것이다. 이제 5 x 5 필터커널을 가지고 좌측상단부터 보폭1로 컨볼루션을 진행해준다.

5 x 5 필터커널은 우로 이동하면서 총 7번의 컨볼루션 연산을 진행하고, 또한 아래로 이동하면서 총 7번의 컨볼루션 연산을 진행한다. 따라서 7 x 7 특성맵이 산출되는 것이다.
만약 컨볼루션 보폭이 2라면 두 칸씩 움직이기 때문에, 오른쪽 끝에 도달할 때까지 4번, 아래 끝에 도달할 때까지 4번 컨볼루션 연산이 진행된다. 이때는 4 x 4 특성맵이 산출된다.

이것을 일반화하면 다음과 같은 공식이 만들어진다. 입력 이미지의 크기가 H x W이고, zero padding을 P만큼 해주고, 필터의 크기가 $F_H$ x $F_W$이고, 컨볼루션 보폭(stride)이 S라면, 특성맵의 높이와 너비는 각각
$Feature \: Map \: Height = \frac{H + 2P - F_H}{S} + 1$
$Feature \: Map \: Width = \frac{W + 2P - F_W}{S} + 1$
이 된다.
공식이 잘 작동하는지 확인해보자. 9 x 9 이미지에 zero padding을 1만큼 해주고, 필터의 크기가 5 x 5이고, 보폭이 1일 때 특성맵의 높이 및 너비는
(9 + 2 - 5)/1 + 1 = 6/1 + 1 = 7
이므로 위에서 구한 7 x 7과 동일하다. 또한 동일한 조건에 보폭만 2로 바꿨을 때 특성맵의 높이 및 너비는
(9 + 2 - 5)/2 + 1 = 6/2 + 1 = 4
이므로 위에서 구한 4 x 4와 동일하다. 공식이 잘 작동됨을 확인했다.
-----
오늘은 VGG-F, VGG-M, VGG-S의 구조에 대해서 살펴봤습니다. 다음에는 VGG16, VGG19에 대해서 포스팅하도록 하겠습니다. 여기까지 열심히 읽어준 분들께 감사의 말씀을 드립니다.^^
<참고자료>
[1] http://taewan.kim/post/cnn/, TAEWAN.KIM 블로그, "CNN, Convolutional Neural Network 요약"
[2] http://www.vlfeat.org/matconvnet/models/imagenet-vgg-f.svg, VGG-F 상세 구조도
'Research > ML, DL' 카테고리의 다른 글
| 가장 간단한 군집 알고리즘, k-means 클러스터링 (0) | 2019.10.09 |
|---|---|
| 유유상종의 진리를 이용한 분류 모델, kNN(k-Nearest Neighbor) (6) | 2019.10.08 |
| [CNN 알고리즘들] GoogLeNet(inception v1)의 구조 (19) | 2019.10.07 |
| [CNN 알고리즘들] VGGNet의 구조 (VGG16) (26) | 2019.06.28 |
| [CNN 알고리즘들] AlexNet의 구조 (17) | 2019.03.11 |
| 딥러닝에 사용되는 softmax 함수 (0) | 2019.03.08 |
| 이미지 분류 모델 평가에 사용되는 top-5 error와 top-1 error (11) | 2019.03.06 |
| [CNN 알고리즘들] LeNet-5의 구조 (12) | 2019.03.06 |