안녕하세요. 비스카이비전입니다. 오늘은 이진 분류기의 성능을 평가하는데 널리 사용되는 AUC 성능지표에 대해서 알아보도록 하겠습니다.
우선 이진 분류기(binary classifier)는 양성과 음성, 1과 0, +와 -, 앞과 뒤와 같이 두 가지의 클래스를 분류할 수 있는 분류기를 뜻합니다. 이진 분류기의 성능을 평가하는데 사용되는 것 중 하나가 AUC입니다.
AUC
AUC, 또 다른 말로 AUROC는 area under the ROC (receiver operating characteristic) curve의 약어입니다. ROC 곡선(커브) 아래 부분의 넓이로 해석하면 정확합니다. 그 넓이값이 이진 분류기의 성능을 평가하는데 사용된다는 것입니다. 도대체 왜 그럴까요? 그러면 먼저 ROC 곡선이 무엇인지 알아야겠죠?
ROC
ROC 곡선은 다음과 같이 생겼습니다.
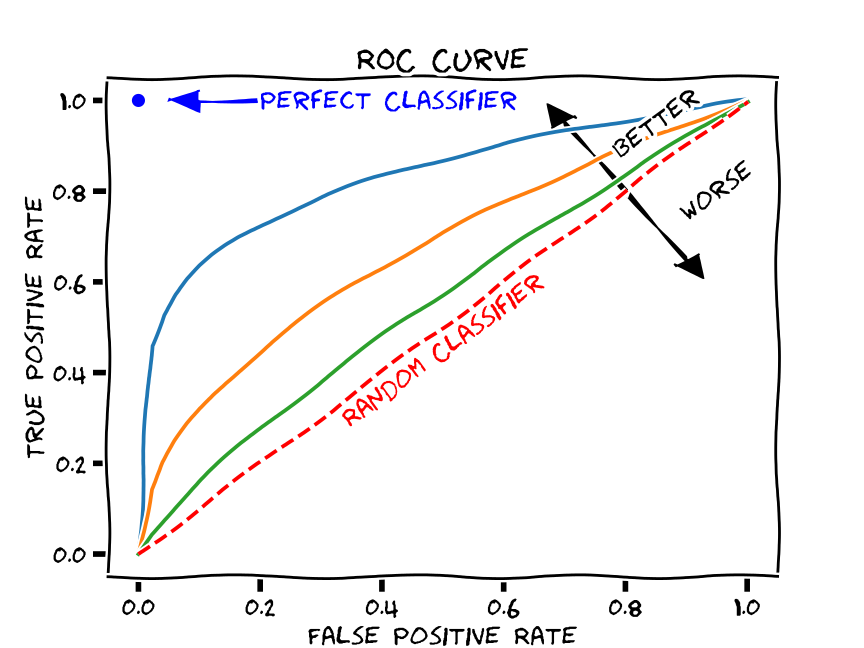
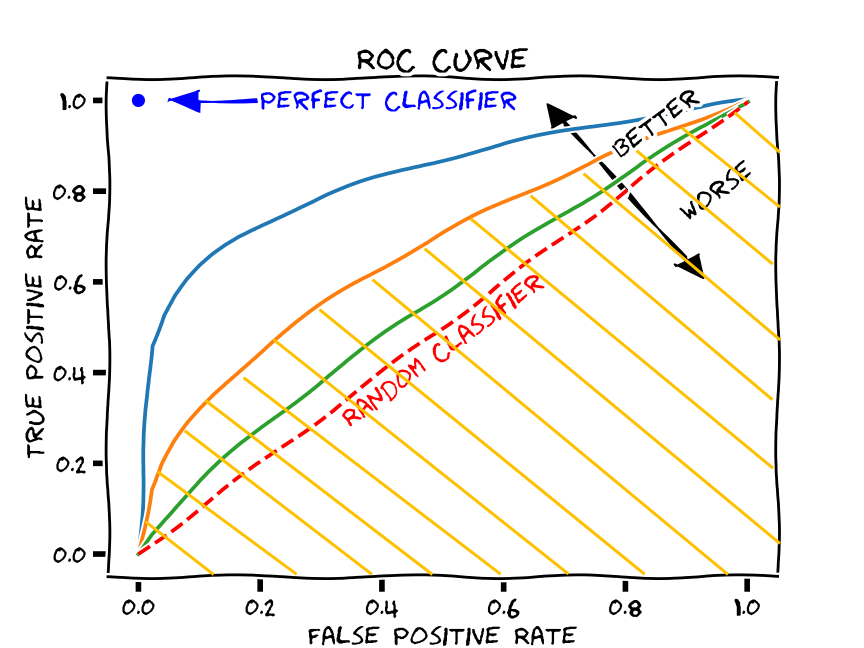
ROC가 뭐가 뭔진 몰라도 아까 AUC는 ROC 커브 아래의 넓이라고 했으니까, 아래와 같이 색칠된 부분의 넓이를 의미하는 것이겠죠? (주황색의 ROC 커브일 때를 예로 들었습니다.)
ROC 커브를 이해하려면 우선 x축과 y축에 있는 true positive rate (TPR)와 false positive rate (FPR)를 알아야 합니다. 또한 TPR과 FPR을 이해하려면 TP (true positive), FP (false positive), TN (true negative), FN (false negative)을 알아야 합니다. 알아야할 게 참 많죠?ㅜㅠ 그래도 포기하지 말고 끝까지 한 번 읽어봅시다. 분명 수확이 있을 것입니다.
TP, FP, TN, FN

TP는 양성인 샘플이 이진 분류기에 의해 양성으로 옳게 분류된 것을 의미합니다. 암환자가 암환자로 판정나는 경우가 여기에 속합니다. (암의 존재를 정확히 발견했으니 치료 잘 받으면 됩니다.)
FP는 음성인 샘플이 양성으로 잘못 분류된 것을 의미합니다. 암환자가 아닌데 암환자로 판정나는 경우가 FP입니다. (보험금은 타지만, 실제로는 건강한 것이니 땡큐죠.)
FN은 양성인 샘플이 음성으로 잘못 분류된 것을 말합니다. 암환자인데 암환자가 아닌 것으로 판정나는 경우가 FN입니다. (이런 경우가 가장 위험하죠. 암이 점점 더 전이될 것입니다.)
TN은 음성인 샘플이 음성으로 옳게 분류된 것을 말합니다. 암환자가 아닌데 암환자가 아닌 것으로 판정나는 것이 TN입니다. (건강한 사람이 건강하다고 판정난 경우니 좋습니다.)
TP와 TN은 많고, FP와 FN은 적어야 좋은 성능을 가진 이진 분류기라고 말할 수 있겠죠? T가 들어간 놈들은 좋은 놈들이고, F가 들어간 놈들은 나쁜 놈들입니다.
TPR과 FPR
우리가 알고 싶었던 것은 ROC 곡선 그래프의 y축인 TPR과 x축인 FPR입니다. 우선 TPR은 다음과 같이 계산합니다.
$ TPR = \frac{TP}{all \: positive} = \frac{TP}{TP + FN} $
그러니까 TPR이라는 것은 전체 양성 샘플 중에 양성으로 예측된 것의 비율을 나타냅니다. TP와 FN은 어떻게 예측되었든 상관없이 모두 실제로는 양성 샘플임을 기억하세요. TP가 많고 FN이 적을수록 TPR은 1에 가까워집니다.
반면, FPR은 다음과 같이 계산합니다.
$ FPR = \frac{FP}{all \: negative} = \frac{FP}{FP + TN} $
FPR은 전체 음성 샘플 중에 양성으로 잘못 예측된 것의 비율을 나타냅니다. FP가 적고 TN이 많을수록 FPR은 0에 가까워집니다.
정리하자면, TPR은 1에 가까울 수록 좋고, FPR은 0에 가까울 수록 좋습니다.
decision threshold
이제 decision threshold라는 것을 다룰 차례입니다. 이진 분류기의 경우 0과 1사이의 값을 산출해냅니다. 그 값은 테스트 샘플이 양성일 확률을 나타냅니다. 그 값이 얼마 이상일 때 양성으로 판정을 내릴지에 대한 기준값이 필요합니다. 그 기준값이 바로 decision threshold입니다. 그냥 단순히 0.5로 설정할 수도 있지만, 필요에 따라 Decision threshold를 높여야 하는 경우도 있고 낮춰야 할 때도 있습니다.
decision threshold를 높게 한다면 양성으로 판정되는 경우가 적어질 것입니다. 조금 보수적으로 예측하는 것이죠. 반면, decision threshold를 낮게 잡는다면, 양성으로 판정되는 경우가 많아질 것입니다. 다소 공격적으로 예측하는 것이죠.
decision threshold를 0, 0.1, 0.2, 0.3,..., 0.8, 0.9, 1로 바꿔가면서 그때마다의 TP, FP, FN, TN을 계산해서 TPR과 FPR을 기록해둡니다. 그러면 다음과 같은 기록이 쌓일 것입니다.

참고로 decision threshold가 0이면 이진분류기는 무조건 양성으로 분류합니다. 왜냐하면 이진분류기는 0과 1사이의 값을 산출하기 때문입니다. 따라서, 음성으로 예측되어야 존재 가능한 TN과 FN은 모두 0이 됩니다. 결과적으로 TPR과 FPR은 모두 1이 됩니다.
TPR = TP/(TP + FN) = 50/50 = 1
FPR = FP/(FP + TN) = 50/50 = 1
반면, decision threshold가 1이면 이진분류기는 무조건 음성으로 분류합니다. 따라서, 양성으로 예측되어야 존재 가능한 TP와 FP는 모두 0이 됩니다. 결과적으로 TPR과 FPR은 모두 0이 됩니다.
TPR = 0/50 = 0
FPR = 0/50 = 0
다시 ROC
이제 위 표에 있는 (FPR, TPR)쌍을 그래프에 하나씩 찍어줍니다. 그 점들을 이어준 것이 바로 ROC 곡선이 됩니다.

decision threshold를 1, 0.9999, 0.9998, 0.9997과 같이 좀 더 자잘하게 나눠주면 위보다 좀 더 부드러운 곡선이 될 것입니다.
다시 AUC
이제 고지가 눈 앞입니다. 다 왔습니다. ROC curve를 그렸으니, 이제 그 아래의 넓이를 계산하는 것도 가능합니다. 삼각형과 사다리꼴의 넓이들을 더하는 식으로 계산이 가능하겠죠? 그것을 계산하는 것까지 여기에 굳이 넣진 않겠습니다. 그런데 왜 그 넓이가 넓을수록 이진 분류기의 성능이 좋은 것인지는 한 번 생각해볼 가치가 있습니다.
TPR은 기본적으로 높을 수록 좋습니다. TPR은 전체 양성 샘플 중에 양성으로 예측된 샘플의 비율이기 때문입니다. 하지만, FPR은 낮을 수록 좋습니다. FPR은 전체 음성 샘플 중에 양성으로 잘못 예측된 것의 비율이기 때문입니다.
decision threshold가 커지면 TPR이든 FPR이든 작아질 수 밖에 없습니다. 양성으로 예측되는 경우가 적어지기 때문입니다. 따라서 FPR의 값이 작아질 때 TPR이 천천히 작아진다면, 좋은 성능을 가진 이진분류기라고 볼 수 있습니다. 그런 경우에는 곡선 아래의 넓이가 정사각형의 넓이 1 x 1 = 1에 가까워질 것입니다. 그렇기 때문에 AUC, 즉 ROC 곡선 아래의 넓이를 통해 이진분류기의 성능을 평가할 수 있는 것입니다.
대개 AUC가 0.8이상이면 아주 훌륭한 성능을 가진 이진분류기라고 평가합니다. 0.7과 0.8 사이라면 좋은 이진분류기입니다. AUC가 0.5~0.7라면 있으면 도움은 되는 이진분류기입니다. AUC가 만약 0.5이하라면 쓸모없는 이진분류기입니다. 없는 것만 못합니다.
끝까지 읽으시느라 수고하셨습니다. 도움이 되셨길 바라며 글을 맺겠습니다. :D
관련 글
물체 검출 알고리즘 성능 평가방법 AP(Average Precision)의 이해
[python] 쉽고 간단하게 마스크 착용 유무 판별기 만들기
참고자료
[1] glassboxmedicine.com/2019/02/23/measuring-performance-auc-auroc/, GLASS BOX, "Measuring Performance: AUC (AUROC)"
[2] glassboxmedicine.com/2019/02/17/measuring-performance-the-confusion-matrix/, GLASS BOX, "Measuring Performance: The Confusion Matrix"
[3] angeloyeo.github.io/2020/08/05/ROC.html, 공돌이의 수학정리노트, "ROC curve"
(이 글은 2021-5-1에 마지막으로 수정되었습니다)
'Research > ML, DL' 카테고리의 다른 글
| 단순회귀분석 vs 다항회귀분석 vs 다중회귀분석 (0) | 2022.09.05 |
|---|---|
| 정규화(normalization)와 표준화(standardization), 머신러닝 성능 향상을 위한 필수 단계 (4) | 2020.07.13 |
| 오차 역전파(error backpropagation) 개념 제대로 파악하기 (57) | 2020.07.02 |
| 딥러닝 손실 함수(loss function) 정리: MSE, MAE, binary/categorical/sparse categorical crossentropy (4) | 2020.06.24 |
| 배치(batch)와 에포크(epoch)란? (5) | 2020.06.11 |
| ground-truth 라벨을 얻기 어려운 경우 대안, pseudo 라벨 (0) | 2020.04.15 |
| 손실함수(loss)와 평가지표(metric)란? 그 차이는? (0) | 2020.04.07 |
| hold-out 교차검증과 k-fold 교차검증 (2) | 2020.03.16 |