관련 글
자료를 대표하는 숫자, 대표값: 평균, 중앙값, 최빈값
오늘은 pandas 데이터프레임의 기술 통계 정보를 요약해주는 describe() 메소드에 대해 소개드리도록 하겠습니다. 기술통계란 수집한 데이터의 특성을 표현하고 요약해주는 통계 기법을 의미합니다. 평균, 분산, 표준편차, 중앙값 등이 기술통계에 속합니다. 데이터프레임의 describe() 메소드를 활용하면 평균, 표준편차, 최대값, 최소값 등의 기술통계 정보를 한번에 요약해서 보여줍니다.
seaborn 패키지는 테스트를 위한 여러 데이터셋을 제공하는데 그 중 하나인 car_crashes 데이터셋을 오늘 예제에 활용하도록 하겠습니다. car_crashes 데이터셋은 자동차 사고와 관련된 데이터를 담고 있습니다. 총 51개의 행과 8개의 컬럼으로 구성되어 있는데, 51개 행은 미국의 51개 주를 의미하고, 8개의 컬럼은 각각 다음을 의미합니다. 영어 문서를 보면서 번역한 내용인데 저 스스로 독해가 완벽히 되지 않은 것들은 추가로 영어 원문도 남겨놨습니다.
1. total
10억 마일당 치명적인 충돌에 연루된 운전자의 수
2. speeding
과속으로 인해 치명적인 충돌에 연루된 운전자의 비율
3. alcohol
음주로 인해 치명적인 충돌에 연루된 운전자의 비율
4. not_distracted
주시 태만이 아니지만 치명적인 충돌에 연루된 운전자의 비율(Percentage Of Drivers Involved In Fatal Collisions Who Were Not Distracted)
5. no_previous
이전에 어떠한 사고와도 연루되지 않았지만 치명적인 충돌에 연루된 운전자의 비율
6. ins_premium
자동차 보험료
7. ins_losses
보험을 든 운전자 1인당 충돌 사고로 인해 보험사가 입은 손해
8. abbrev
미국의 주 이름 약자
자, 이제 위 데이터셋을 판다스 데이터프레임으로 불러오고, describe 메소드를 활용하여 기술 통계 정보를 확인해보도록 하겠습니다. 필요한 파이썬 코드는 다음과 같습니다.
import seaborn as sns
df_car_crashes = sns.load_dataset('car_crashes')
print(df_car_crashes, '\n')
print(df_car_crashes.describe())
코드를 실행하면 다음과 같은 내용이 콘솔에 출력됩니다.
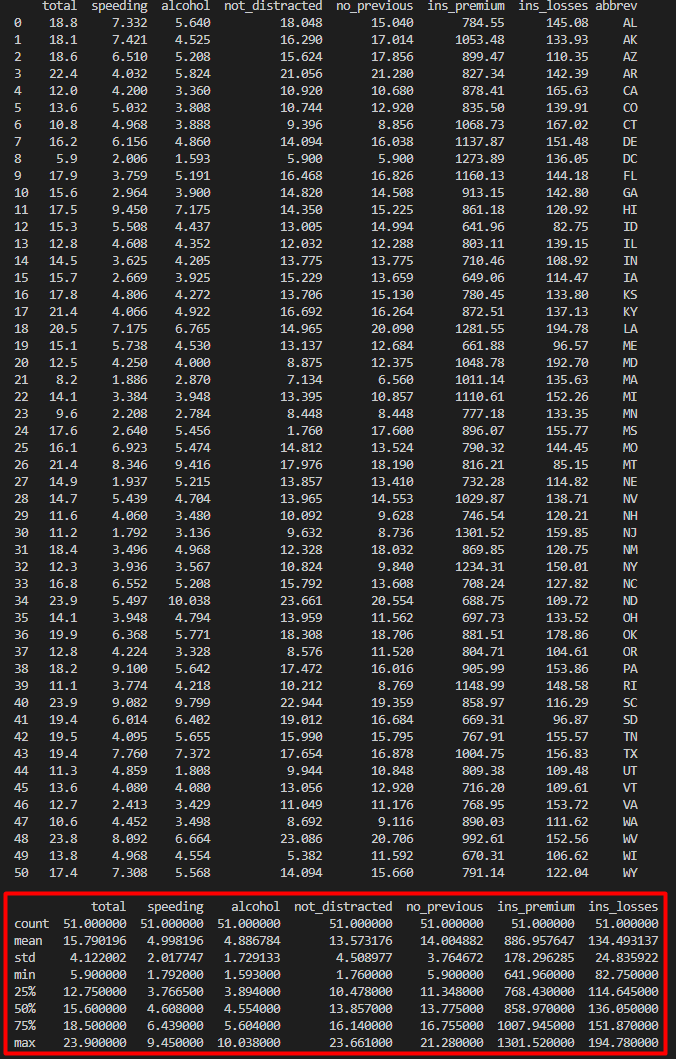
빨간색으로 강조한 부분이 describe() 메소드로 인해 출력된 데이터프레임 기술 통계 정보입니다. 각 컬럼의 count (데이터 개수), mean (평균), std (표준편차), min (최소값), 25% (제1사분위수), 50% (제2사분위수), 75% (제3사분위수), max (최대값)이 각각 출력된 것을 확인하실 수 있습니다.
total 컬럼의 기술 통계 정보만 살펴보자면, total 컬럼의 데이터 개수는 51개, 데이터의 평균은 15.79, 표준편차는 4.12, 최소값은 5.9, 제1사분위수는 12.75, 제2사분위수는 15.6, 제3사분위수는 18.5, 최대값은 23.9인 것입니다.
평균, 표준편차, 최소값, 최대값은 아시는 분들이 많지만 제1사분위수, 제2사분위수, 제3사분위수라는 용어는 생소하신 분들도 계실 것입니다.
분위수는 n개의 데이터를 작은 수부터 큰 수의 순으로 정렬해놓고(오름차순 정렬), 그것을 k 등분했을 때, 그 경계가 된 수치를 뜻합니다[2]. 4등분을 했다면 제1사분위수, 제2사분위수, 제3사분위수가 있는 것인데, 4등분된 데이터에서 1번째 그룹과 2번째 그룹의 경계가 된 값이 바로 제1사분위수가 되고, 2번째 그룹과 3번째 그룹의 경계가 된 값이 제2사분위수가 되고, 3번째 그룹과 4번째 그룹의 경계가 된 값이 제3사분위수가 됩니다. 아래 이미지를 참고하시면 조금 더 이해가 쉬우실 것입니다.

제2사분위수는 중앙값(median)이라고도 부릅니다. 말그대로 데이터에서 중앙에 위치하기 때문에 중앙값입니다. 또한 사분위 범위라는 것도 있는데 제3사분위수와 제1사분위수의 차를 뜻합니다. 데이터가 중앙값 근처에 모여있을 수록 사분위 범위는 작아집니다[2].
데이터프레임의 describe() 메소드를 이용하면 이렇게 쉽게 데이터의 특성을 한 눈에 확인할 수 있다니 정말 좋죠? ㅎㅎ
참고자료
[1] https://senolomer0.medium.com/seaborn-datasetss-explorations-39d080e55e55, seaborn 데이터셋들 소개
[2] 쿠리하라 신이치, 마루야마 아츠시 지음, "통계학 도감", 성안당(2018)
'Dev > python' 카테고리의 다른 글
| [pyside6] 창 타이틀바에서 닫기 버튼, 최소화 버튼, 최대화 버튼 등을 비활성화 되게 하려면? (0) | 2022.06.07 |
|---|---|
| [python+pandas] 일간 데이터를 월간 데이터로 변환한 후에 선 그래프 그리기 (5) | 2022.06.06 |
| [pandas] 선 그래프, 막대 그래프, 히스토그램, 박스 플롯 그리기 (0) | 2022.06.05 |
| [pandas] 튜플의 리스트를 데이터프레임으로 만들기 (0) | 2022.05.30 |
| [python+pandas] 여러 데이터프레임 하나의 엑셀 파일 내 각각 다른 시트에 저장하기 (5) | 2022.05.15 |
| [python] seaborn 라이브러리가 제공하는 타이타닉 데이터셋 설명 (0) | 2022.05.15 |
| [pandas] 데이터프레임 groupby(), agg() 메소드로 그룹의 평균값, 최대값 산출하기 (0) | 2022.04.28 |
| [python+pandas] 판다스 데이터 프레임에서 컬럼의 고유값을 알고 싶으면, unique 메소드 (0) | 2022.04.27 |