그레디언트 기반 엣지 연산자들(Sobel, Canny 등)은 밝기 및 콘트라스트 변화에 취약하다. 이말인즉슨 두 이미지가 내용은 같고 단순히 밝기 또는 콘트라스트만 다르더라도, 검출된 엣지에 차이가 발생한다는 것이다. 반면 위상 합동(Phase congruency)을 이용해서 엣지를 검출하면 밝기(brightness)와 콘트라스트(contrast) 변화에 영향을 받지 않는다. 그 이유에 대해 살펴보자. 결론적으로 말하자면 픽셀 영역이 아닌 주파수 영역에서 엣지를 검출해내기 때문이다.
먼저 1차원 신호를 예를 들어 위상 합동의 개념에 대해 이해해보자. 시간 $x$일때의 1차원 신호는 각각의 진폭(amplitude)과 위상(phase)을 지닌 여러 코사인 곡선들(각기 다른 주파수들을 가짐)의 합으로 표현할 수 있다.
$I(x) = \sum_n A_n(x)cos{\phi_n(x)}$
여기서 $A_n$은 크기를 나타내고 $\phi_n$은 위상을 나타낸다. 참고로 위상은 곡선이 얼마나 출발점에서 떨어져 있는 지를 나타낸다. 아래 그림은 빨간색 신호는 파란색인 코사인들의 합으로 분해할 수 있다는 보여준다.
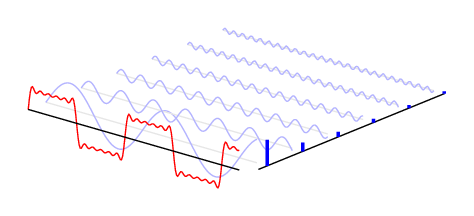
각 코사인을 크기(amplitude)와 방향(phase)을 가진 벡터로 표현한 후 합해준다면(벡터의 합), 극좌표계에서 다음과 같이 표현될 것이다.
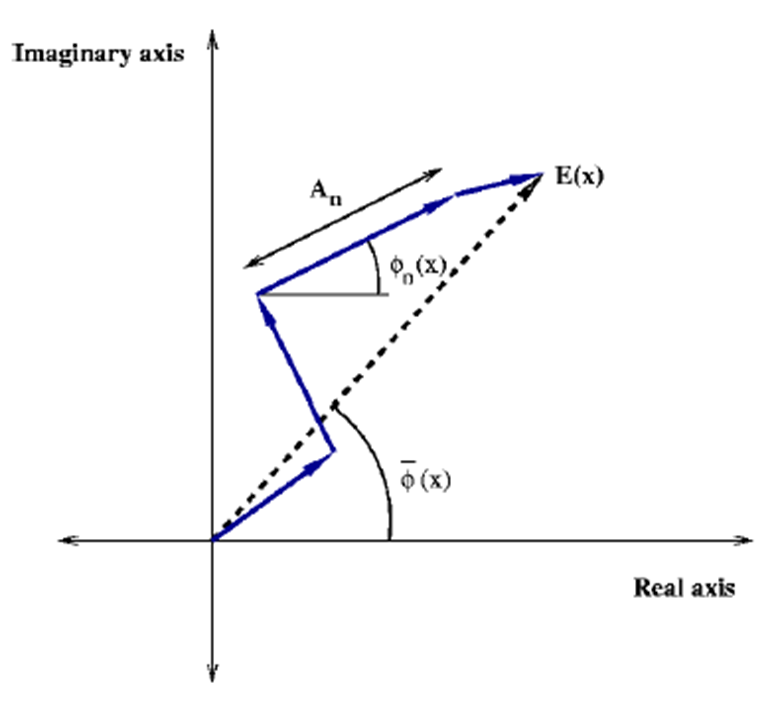
여기서 모든 벡터들을 합한 결과 벡터인 $E(x)$는 로컬 에너지라고 불린다. 만약 벡터들의 방향(위상)이 유사하면 유사할수록 $E(x)$의 크기는 커질 것이다. 일관된 방향으로 계속 쭉쭉 뻗어나가기 때문이다. 이러한 현상을 위상 합동이라고 부른다. 따라서 위상 합동(phase congruency, PC)의 정도는 다음과 같은 식으로 나타낼 수 있다.
$PC(x) = \frac{|E(x)|}{\sum_n A_n(x)}$
로컬 에너지 E(x)를 모든 진폭을 합한 것으로 나눠주는 것이다. 만약 모든 벡터의 방향이 같은 경우라면 $|E(x)| = \sum_n A_n(x)$가 되어 PC는 1이 될 것이다. 반면 방향이 많이 다르고 서로 역방향인 경우도 많다면 0에 가까워진다. 따라서 $0 \leq PC(x) \leq 1$이다.
이것을 확장시켜 2차원인 이미지 신호에 적용하면, 우리는 결과적으로 2차원 PC 맵을 얻게 된다. 1차원 때와 마찬가지로 값이 1에 가까운 위치는 위상 합동의 정도가 크다는 것이고, 즉 로컬 에너지가 센 부분이라는 의미를 갖게 된다. 로컬 에너지가 센 부분을 픽셀 영역에서 살펴보면 엣지 또는 코너가 된다. 따라서 이 위상 합동을 이용해서 엣지 검출이 가능한 것이다.
아래 그림은 이미진 내에서 위상 합동이 어떤 의미를 갖는지를 나타내준다. 신호들의 위상이 일치하는 부분들이 엣지라는 것이다.

그러면 콘트라스트만 다른 두 이미지에서 그레디언트 기반 엣지 연산자와 위상 합동 기반 엣지 방법으로 산출된 엣지 맵들을 비교해보자. 그레디언트 기반 엣지 연산자로는 Sobel를 사용했고, 위상 합동 기반 엣지 방법으로는 [4]에서 제시된 방식을 활용했다. 테스트를 위해 사용한 이미지는 다음과 같다.

왼쪽 이미지가 오른쪽 이미지에 비해 좀 더 높은 콘트라스트를 지니고 있다. Sobel와 PC를 이용해서 얻은 엣지 맵들은 아래와 같다. PC 엣지 맵의 경우 값들이 0에서 1사이를 가지므로 표준화(normalization)없이 그레이 영상으로 표현이 가능하지만, Sobel 엣지 맵은 전시를 위해서는 표준화가 필요하다.

표준화된 Sobel 엣지 맵들을 봐서는 차이를 못느끼겠다. 하지만 아래 표에서 표준화 전 실제값들을 보면 분명 차이가 있음을 알 수 있다. 반면 PC 엣지 맵들은 값에 있어서 거의 차이가 없다. 이로써 우리는 PC 엣지 맵이 밝기 및 콘트라스트 불변 특징을 지님을 알 수 있다.
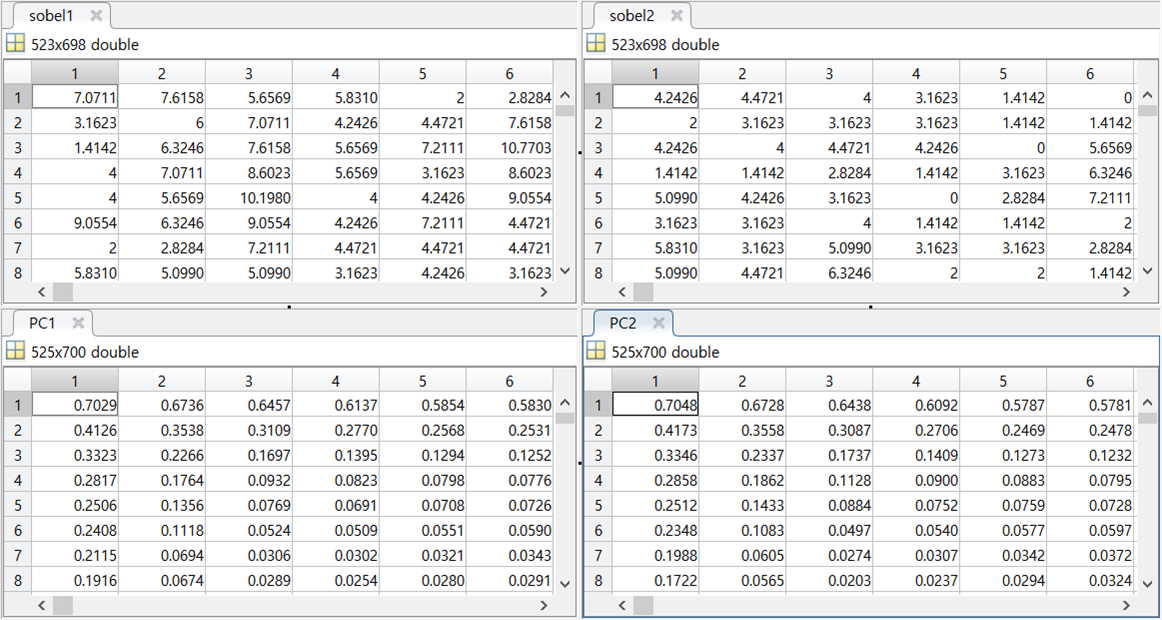
픽셀 영역에서 밝기 차이를 이용해 엣지를 검출해내는 그레디언트 기반 연산자들과는 달리, 위상 합동 방식은 주파수 영역에서 엣지를 검출해낸다. 이것을 머릿 속에 꼭 기억하자.
혹시 제 이해가 잘못되었거나 불충분한 부분이 있다면 댓글로 한수 알려주시길 부탁드립니다.^^
<참고자료>
[1] https://en.wikipedia.org/wiki/Phase_congruency, 위키피디아(영문), "Phase congruency"
[2] http://cvpr11.cecs.anu.edu.au/files/PhaseCongCVPR.pdf, Kovesi, "Image Features from Phase Congruency"
[3] http://www.robots.ox.ac.uk/~jmb/lectures/TransformLectures.pdf, "Advanced transform methods"
[4] Peter Kovesi, "Image Features from Phase Congruency", VIDERE: Journal of Computer Vision Research (1999)
[5] http://pgfplots.net/tikz/examples/fourier-transform/, PGFPlots.net, "Example: Fourier transform"
'Research > 컴퓨터비전, 영상처리' 카테고리의 다른 글
| [Visual saliency] 예상되는 주파수 정보는 시각적으로 중요하지 않다, SRVS (1) | 2019.11.07 |
|---|---|
| [IQA] 콘트라스트 변화에 의한 품질의 변화를 고려한 알고리즘, RIQMC (0) | 2019.11.06 |
| [IQA] DoG 분해를 활용한 학습 기반 이미지 품질 평가 알고리즘, DOG-SSIM (0) | 2019.11.01 |
| [IQA] visual saliency를 활용한 이미지 품질 평가 알고리즘, VSI (7) | 2019.10.30 |
| [Visual saliency] 그래프 기반 visual saliency 알고리즘, GBVS (0) | 2019.10.14 |
| [IQA] 왜곡으로 인한 artifact를 블러, 노이즈, 블락으로 분류해서 다룬 BNB (0) | 2019.10.07 |
| 슈퍼픽셀(superpixel)과 SLIC 알고리즘 활용 (0) | 2019.09.30 |
| 전역 선행성(global precedence)이란? (0) | 2019.09.03 |