랜덤 포레스트(Random Forest)에 대해서 알고 싶어서 조사를 하다보니 결정 트리(Decision Tree)에 대한 선지식이 필요함을 알게 되었다. 이름을 보니 무언가 감이 오지 않는가? 포레스트(숲)와 트리(나무). 수많은 나무들로 이뤄진 것을 보통 숲이라고 한다. 즉 랜덤 포레스트는 여러 개의 결정 트리를 함께 활용해 더 나은 성능을 발휘하는 알고리즘이라고 볼 수 있다. 자, 그럼 그 숲을 구성하는 나무, 결정 트리에 대해서 알아보자.
결정 트리란?
결정 트리는 스무고개 게임과 유사한 원리를 갖고 있다. 스무고개 게임은 답을 맞추기 위해 '예', '아니오'로 대답할 수 있는 질문을 최대 20번 할 수 있는 게임이다. 마찬가지로 결정 트리의 핵심도 질문이다. 질문을 통해 답을 찾아가는 것이다. 아래 그림을 보자.

네 종류의 동물 비둘기, 닭, 사슴, 개를 구분한다고 생각해보자. 네 동물 중 비둘기와 닭은 날개가 있고 사슴과 개는 날개가 없으므로 첫 질문으로 날개의 유무를 선택했다. 그 다음에 비둘기와 닭 중에 비둘기만 날 수 있으므로 비행의 가능성을 그 다음 단계의 질문으로 선택했다. 또한 사슴과 개 중에 사슴만 뿔이 있으므로 뿔의 유무를 질문으로 선택했다. 이런 식으로 잘 분류할 수 있는 질문들을 위에서 아래로 하나하나 설정하는 것이 결정 트리의 핵심이다.
ID3 알고리즘
1986년 로스 퀸란에 의해 개발된 ID3는 결정 트리의 가장 초창기 모델 중 하나다. 위에서 언급한 대로 결정 트리의 핵심은 변별력이 좋은 질문을 위에서부터 하나하나 세팅하는 것인데, 이를 위해서 ID3는 정보 이론의 정보량과 엔트로피를 활용했다.
정보량이란 어떤 사건이 가지고 있는 정보의 양인데, 드물게 발생하는 일일수록 정보량이 크다. 일어날 확률이 적은 사건이 일어났을 때 사람들은 많이 놀란다. 따라서 정보량을 놀람의 정도로 표현하기도 한다. 정보량은 다음과 같은 수식으로 나타낸다.
$I(x) = log_2 \frac{1}{p(x)}$
여기서 $p(x)$는 사건 $x$가 발생할 확률이다. 발생할 확률이 1에 가까울수록 정보량은 0에 가까워지고, 발생할 확률이 0에 가까울수록 정보량은 무한히 커진다. 아래 그래프를 보면 무슨 상황인지 확실히 이해가 될 것이다.
엔트로피는 정보량의 기댓값(평균)을 나타낸다. 발생한 사건들의 정보량을 모두 구해서 (가중)평균낸 것이다.
$E(S) = \sum_{i=1}^{c}p_iI(x_i) = \sum_{i=1}^{c}p_ilog_2\frac{1}{p(x_i)} = \sum_{i=1}^{c}p_ilog_2\frac{1}{p_i}$
여기서 $S$는 이미 발생한 사건의 모음을 의미한다. 그리고 $c$는 사건의 갯수다. 엔트로피가 크다는 것은 평균 정보량이 크다는 것인데, 대개 사건들이 일어날 확률이 비슷한 경우에 엔트로피가 크다. 어떤 두 가지 사건이 각각 {0.9, 0.1}의 확률로 일어나는 경우부터 시작해 {0.8, 0.2}, {0.7, 0.3},..., {0.2, 0.8}, {0.1, 0.9}로 일어나는 경우의 엔트로피를 비교해보자. 그 결과 엔트로피의 변화를 나타낸 그래프는 다음과 같다.
두 사건이 0.5, 0.5 확률로 일어날 때의 엔트로피가 가장 크다는 것을 알 수 있다. 50:50의 확률이므로 어떤 사건이 일어날지 모른다. 즉, 불확실성이 클수록 엔트로피가 크다. 불확실성이 크면 클수록 분류하기는 어려워진다. 따라서 우리는 엔트로피가 가장 작은 것을 상위 의사결정 노드에 위치시켜야 한다. 이것이 바로 ID3의 핵심 포인트다.
이를 위해 ID3에서는 정보획득이라는 개념을 들여놓았다. 정보획득량은 다음과 같이 계산한다.
$IG(S, A) = E(S) - E(S|A)$
여기서 A는 속성을 의미한다. 어떤 속성을 가지고 분류했을 때 가장 엔트로피가 작은지, 즉 정보획득량이 큰지를 알아내야한다. 이것이 무슨 말인지는 하나의 예제를 들어서 설명하도록 하겠다.
ID3 알고리즘 설명 예제
아래는 기상 조건들에 따라 테니스 경기 참가 여부를 분류하는 결정 트리 예제다.

먼저 목표 속성인 경기 참가에 대한 엔트로피를 구한다. 참가횟수가 총 9회이고 불참횟수가 5회이므로 참가할 확률은 9/14, 불참할 확률은 5/14이다. 따라서 경기 참가에 대한 엔트로피는 다음과 같다.

자, 이제 어떤 속성을 첫번째로 선택할 때 가장 엔트로피가 작은지, 즉 정보획득량이 큰지 하나씩 살펴보자. 먼저 날씨가 주어졌을 때 경기 참가에 대한 엔트로피(조건부 엔트로피)를 구해보자.
E(경기|날씨) = 맑음 확률*E(경기|맑음) + 흐림 확률*E(경기|흐림) + 비 확률*E(경기|비)

이번에는 온도가 주어졌을 때 경기 참가에 대한 엔트로피를 구해보자.
E(경기|온도) = 더움 확률*E(경기|더움) + 포근 확률*E(경기|포근) + 서늘 확률*E(경기|서늘)

이어서 습도가 주어졌을 때 경기 참가에 대한 엔트로피를 구해보자.
E(경기|습도) = 높음 확률*E(경기|높음) + 정상 확률*E(경기|정상)
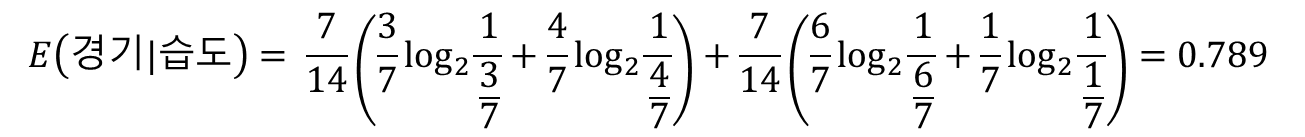
마지막으로 바람이 주어졌을 때 경기 참가에 대한 엔트로피를 구해보자.
E(경기|바람) = 강함 확률*E(경기|강함) + 약함 확률*E(경기|약함)

이중 E(경기|날씨)가 가장 작으므로, IG(경기, 날씨)가 가장 크다.
IG(경기, 날씨) = E(경기) - E(경기|날씨) = 0.94 - 0.694 = 0.246
IG(경기, 온도) = E(경기) - E(경기|온도) = 0.94 - 0.911 = 0.029
IG(경기, 습도) = E(경기) - E(경기|습도) = 0.94 - 0.789 = 0.151
IG(경기, 바람) = E(경기) - E(경기|바람) = 0.94 - 0.892 = 0.048
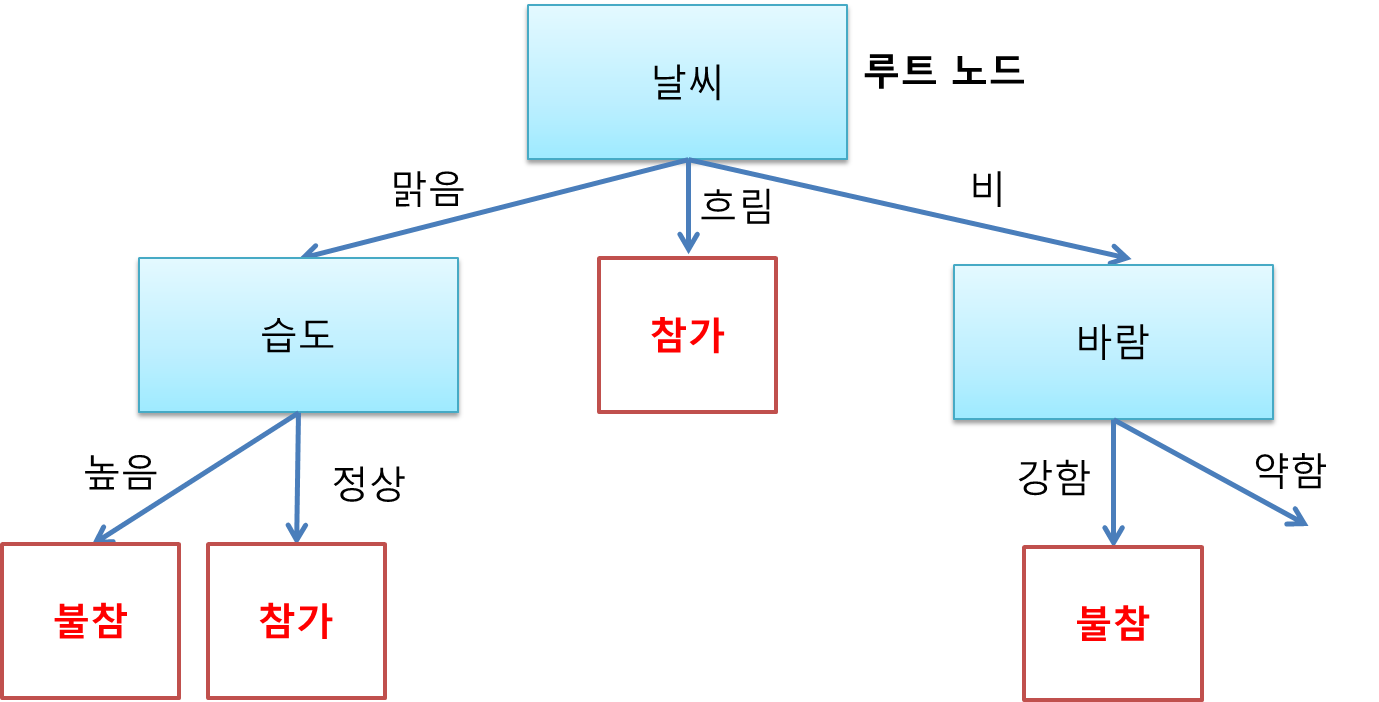
따라서 날씨를 결정 노드로 정해준다. 첫 결정 노드이므로 루트 노드(root node, 뿌리 노드)라고 명명한다.

이제 날씨를 상위 노드의 속성으로 놓고 맑음으로 갔을때(속성값이 맑음일때) 하위노드가 무엇이 될지 찾아보자. 여기서는 맑음인 경우만 생각하면 된다.

목표 속성인 경기 참가의 엔트로피는 다음과 같다. 참가횟수가 2회이고 불참횟수가 3회이므로 참가할 확률은 2/5, 불참할 확률은 3/5이다.

그리고 온도가 주어졌을 때 경기 참가의 엔트로피, 습도가 주어졌을 때 경기 참가의 엔트로피, 바람이 주어졌을 때 경기 참가의 엔트로피를 각각 구하면 다음과 같다.
E(경기|온도) = 더움 확률*E(경기|더움) + 포근 확률*E(경기|포근) + 서늘 확률*E(경기|서늘)

E(경기|습도) = 높음 확률*E(경기|높음) + 정상 확률*E(경기|정상)

E(경기|바람) = 강함 확률*E(경기|강함) + 약함 확률*E(경기|약함)

이중에서 E(경기|습도)가 가장 작으므로, IG(경기, 습도)가 가장 크다.
IG(경기, 온도) = E(경기) - E(경기|온도) = 0.971 - 0.4 = 0.571
IG(경기, 습도) = E(경기) - E(경기|습도) = 0.971 - 0 = 0.971
IG(경기, 바람) = E(경기) - E(경기|바람) = 0.971 - 0.951 = 0.02
따라서 습도를 결정 노드로 정해준다.

이제 날씨를 상위 노드의 속성으로 놓고 흐림으로 갔을때 하위노드가 무엇이 될지 찾아보자. 여기서는 흐림인 경우만 생각하면 된다.

그런데 흐림인 경우에는 항상 참가임을 알 수 있다. 따라서 결정 노드가 아닌 참가 클래스가 붙은 리프 노드(leaf node, 잎 노드)가 아래에 붙는다.

이번엔 날씨를 상위 노드의 속성으로 놓고 비로 갔을때 하위노드가 무엇이 될지 찾아보자. 마찬가지로 비인 경우만 생각하면 된다. 습도 속성은 이미 사용되었으므로 표에서 지웠다.

이때 목표 속성인 경기 참가의 엔트로피는 다음과 같다. 참가횟수가 3회이고 불참횟수가 2회이므로 참가할 확률은 3/5, 불참할 확률은 2/5이다.

그리고 온도가 주어졌을 때 경기 참가의 엔트로피와 바람이 주어졌을 때 경기 참가의 엔트로피를 각각 구하면 다음과 같다.
E(경기|온도) = 포근 확률*E(경기|포근) + 서늘 확률*E(경기|서늘)

E(경기|바람) = 강함 확률*E(경기|강함) + 약함 확률*E(경기|약함)

둘 중에서 E(경기|바람)이 0으로 더 작으므로, IG(경기, 바람)이 더 크다.
IG(경기, 온도) = E(경기) - E(경기|온도) = 0.971 - 0.951 = 0.02
IG(경기, 바람) = E(경기) - E(경기|바람) = 0.971 - 0 = 0.971
그러므로 바람을 결정 노드로 정해준다.
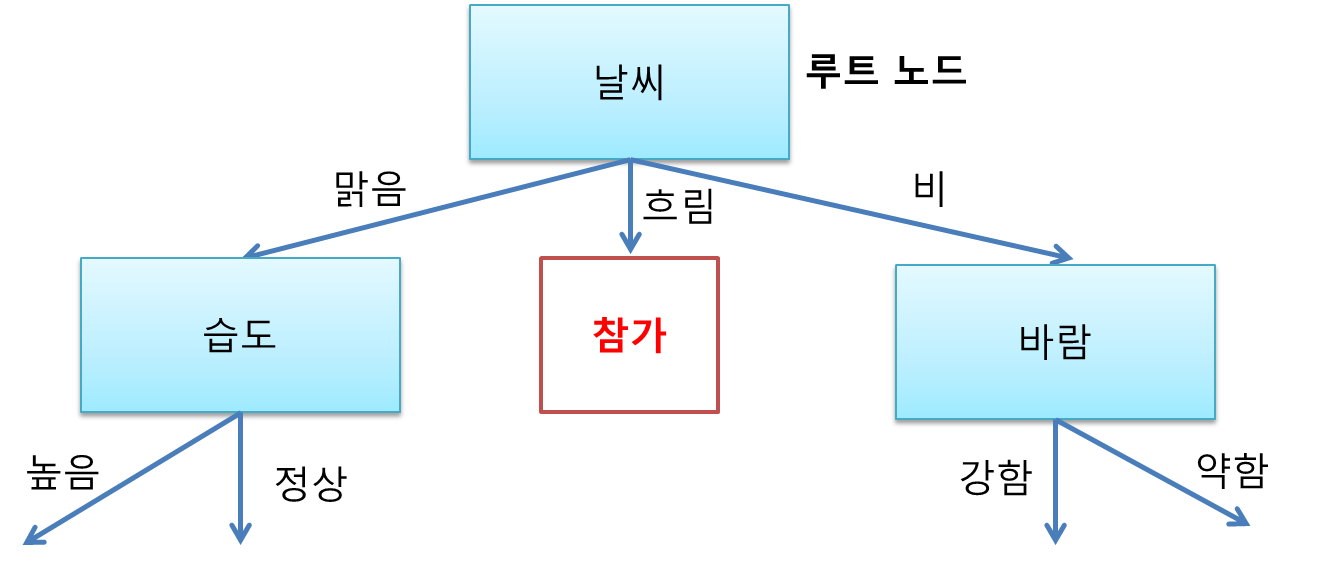
이제 습도를 상위 노드로 놓고 높음으로 갔을 때 하위 노드를 찾아줄 차례다. 날씨 맑음에 습도 높음만 고려해주면 된다.

날씨 맑음에 습도 높음인 날들을 보니 항상 불참했었다. 따라서 습도 높음 가지에는 불참 리프 노드가 붙는다.

이번에는 습도를 상위 노드로 놓고 정상으로 갔을 때 하위 노드를 결정해보자. 날씨 맑음에 습도 정상인 날들만 고려하면 된다.

날씨 맑음에 습도 정상인 경우에는 항상 참가했었다. 따라서 습도 높음 가지에는 참가 리프 노드를 붙여준다.

이번에는 바람을 상위 노드로 놓고 강함으로 갔을 때의 하위 노드를 생각해보자. 날씨 비에 바람 강함인 날들만 고려 대상이다.

이 경우에는 항상 불참했었다. 따라서 바람 강함 가지에는 불참 리프 노드를 붙여준다.
이번에는 바람을 상위 노드로 놓고 약함으로 갔을 때의 하위 노드를 생각해보자. 날씨 비에 바람 약함인 날들만을 고려하면 된다.

이때는 항상 참가했었다. 따라서 바람 약함 가지에는 참가 리프 노드가 붙는다.

모든 가지에 잎이 달렸으므로 드디어 나무 생성이 끝났다. 참고로 온도 속성은 끝내 결정 노드에 쓰이지 않았다. 4개의 속성 중에 가장 변별력이 낮은 속성이었던 것이다.
결정 트리가 생성되었으므로 이제 어떤 날의 기상 컨디션에 따라 테니스 경기를 참가할지 안할지를 분류해낼 수 있다. 아래에 예를 몇개 들어보았다.
흐린 날씨 => 참가
비오는 날씨에 바람이 강하게 붐 => 불참
맑은 날씨에 높은 습도 => 불참
비오는 날씨에 바람이 약하게 붐 => 참가
이런 방식으로 결정 트리 알고리즘 ID3는 작동한다.
끝까지 인내를 갖고 읽어 주셔서 감사합니다. 처음에 결정 트리를 접했을 때는 쉬운 개념이라 생각했는데, 제대로 이해하고 설명하는 것은 결코 쉽지 않네요. 여전히 부족함이 많은 글이지만, 도움이 되셨다면 댓글 또는 공감 부탁드립니다! 또 제가 잘못 이해하고 있는 부분 있다면 지적해주십시오. 혹시 글을 인용하시거나 공유하시는 분들은 꼭 링크로 출처를 남겨주시길 부탁드립니다.^^
<참고자료>
[1] 안드레아스 뮐러, 세라 가이도 지음, 박해선 옮김, "파이썬 라이브러리를 활용한 머신러닝", 한빛미디어(2017)
[2] 김의중 지음, "알고리즘으로 배우는 인공지능, 머신러닝, 딥러닝 입문", 위키북스(2016)
[3] https://en.wikipedia.org/wiki/ID3_algorithm, 위키피디아(영문), "ID3 algorithm"
[4] https://jihoonlee.tistory.com/16, 이지훈님의 블로그, 호옹호옹, "Decision Tree + ID3알고리즘"
[5] https://nittaku.tistory.com/277?category=745644, 동신한의 조재성, "3. 머신러닝 알고리즘: 의사결정 트리(Decision Tree) 알고리즘의 수학적 접근 - ID3 알고리즘"
[6] https://seamless.tistory.com/20, Data Engineer, "의사 결정 트리 (Decision Tree)"
'Research > ML, DL' 카테고리의 다른 글
| 전이학습(transfer learning) 재밌고 쉽게 이해하기 (4) | 2020.02.04 |
|---|---|
| [CNN 알고리즘들] SENet의 구조 (4) | 2020.01.31 |
| [CNN 알고리즘들] ResNet의 구조 (18) | 2019.11.22 |
| 오차(error)와 잔차(residual)의 차이 (2) | 2019.11.20 |
| [강화학습] 마코프 프로세스(=마코프 체인) 제대로 이해하기 (11) | 2019.10.15 |
| 가장 간단한 군집 알고리즘, k-means 클러스터링 (0) | 2019.10.09 |
| 유유상종의 진리를 이용한 분류 모델, kNN(k-Nearest Neighbor) (6) | 2019.10.08 |
| [CNN 알고리즘들] GoogLeNet(inception v1)의 구조 (19) | 2019.10.07 |