결합(joint), 조건부(conditional)라는 단어는 확률에서 많이 쓰이는 용어다. 엔트로피 역시 확률을 이용한 것이므로 결합 엔트로피와 조건부 엔트로피가 존재한다.
엔트로피에 대해 잠시 복습하자. 엔트로피는 평균 정보량이기 때문에 먼저 정보량에 대해 살펴보자. 정보량은 어떤 사건이 가지고 있는 '놀람의 정도'를 나타낸다. 일어날 확률이 적은 사건이 일어났을 때 사람들은 놀란다. 따라서 드물게 일어나는 일일수록 정보량이 크다. 예를 들어, 우리나라가 월드컵에서 우승할 사건의 정보량이 프랑스가 우승할 사건의 정보량보다 훨씬 크다. 왜냐하면 우리나라가 우승할 확률이 프랑스보다는 훨씬 작기 때문이다.
엔트로피는 발생가능한 사건들의 정보량의 평균(기댓값)을 낸 것이다. 따라서 평균 놀람의 정도 또는 불확실성으로 생각할 수 있다. 여러 사건들이 발생할 확률이 비슷할수록 불확실성, 즉 엔트로피는 커진다. 결과가 뻔할수록 엔트로피는 작고, 어떤 결과가 나타날지 예상하기 힘들수록 엔트로피는 크다.
정보량과 엔트로피에 관한 더 자세한 내용은 링크를 참고하자. => https://bskyvision.com/389
결합 엔트로피
이제 결합 엔트로피에 대해 살펴보자. 결합 엔트로피는 두 개 이상의 확률변수들의 결합확률분포의 엔트로피를 뜻한다. 확률변수 X, Y에 대한 결합확률분포표가 다음과 같다고 가정해보자.

확률변수 X, Y의 결합 엔트로피는 H(X, Y)로 나타낸다. 엔트로피를 보통 H라는 기호로 나타낸다. 그리고 다음과 같은 공식을 이용해서 계산한다.
$H(X, Y) = \sum_{x, y}p(x, y)log_2\frac{1}{p(x, y)}$
그러면 실제로 계산해보자. (x, y) = (0, 0)일 확률이 1/4이고, (x, y) = (0, 1)인 확률이 1/4이고, (x, y) = (1, 0)의 확률이 1/2이고, (x, y) = (1, 1)의 확률이 0이므로 다음과 같이 계산된다.
$H(X, Y) = \frac{1}{4}log_2\frac{1}{\frac{1}{4}} + \frac{1}{4}log_2\frac{1}{\frac{1}{4}} + \frac{1}{2}log_2\frac{1}{\frac{1}{2}} + 0log_2\frac{1}{0}=\frac{3}{2}$
조건부 엔트로피
이번에는 조건부 엔트로피에 대해서 생각해보자. X가 주어졌을 때 Y의 엔트로피는 H(Y|X)로 표현하고, Y가 주어졌을 때 X의 엔트로피는 H(X|Y)로 표현한다. 위 확률분포표를 이용해서 두 조건부 엔트로피를 구해보자. 우선 조건부 엔트로피는 다음과 같은 공식으로 계산한다.
$\begin{align*}
H(Y|X) &= \sum _{x}p_X(x)H(Y|X=x)\\
&= \sum _{x}p_X(x)\sum _{y}p_{Y|X}(y|x)log_2\frac{1}{p_{Y|X}(y|x)}
\end{align*}$
여기서 $p_X(x)$와 $p_{Y|X}(y|x)$와 같은 것들은 주변확률 질량함수를 나타낸다. 식으로 보면 복잡하지만 실제로 풀어보면 그렇게 복잡하지 않다. 위 결합확률분포표에 주변확률까지 같이 나타내보자. 횡의 값을 더해서 $p_X(x)$를 구했고, 종의 값을 더해서 $p_Y(y)$를 구했다.
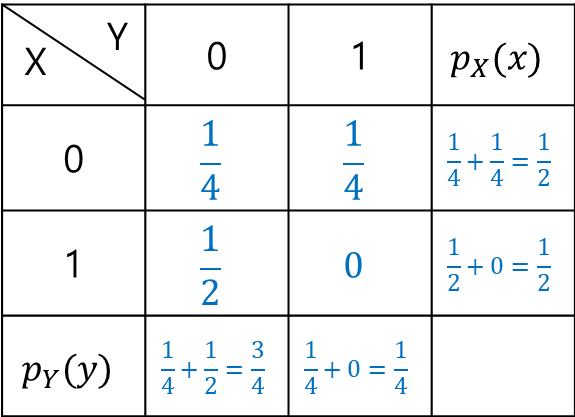
먼저 H(Y|X)부터 구해보자.

이번에는 H(X|Y)를 구해보자.

이것을 통해 우리는 H(Y|X)와 H(X|Y)는 일반적으로 다른 값을 갖는다는 것을 알 수 있다.
<참고자료>
[1] http://www.cs.tau.ac.il/~iftachh/Courses/Info/Fall14/Printouts/Lesson2_h.pdf, "Application of Information theory, Lecture 2, Joint & Conditional Entropy, Mutual Information"
[2] https://mons1220.tistory.com/128, 종혁의 저장소, "[개념] 정보 엔트로피와 그 친구들"
'Research > 확률, 통계' 카테고리의 다른 글
| 이산 확률 분포 정리(균일분포, 이항분포, 포아송분포) (1) | 2022.10.13 |
|---|---|
| 가우시안(정규) 분포와 라플라스 분포의 차이 (14) | 2020.06.12 |
| [정보이론] 상호정보량(mutual information)이란 (3) | 2020.05.15 |
| 직관적으로 쉽게 이해하는 베이즈 정리 (수식은 저리 치워) (2) | 2020.04.15 |
| [정보이론] 정보량과 엔트로피의 의미 (2) | 2019.10.25 |
| kullback-leibler divergence(KL 발산)의 간략한 설명 (14) | 2019.09.09 |
| 자료를 대표하는 숫자, 대표값: 평균, 중앙값, 최빈값 (0) | 2019.06.03 |
| 모평균의 신뢰구간 추정하기 (31) | 2019.05.16 |