선형 회귀가 어떤 데이터 분포를 가장 잘 설명해내는 직선을 찾아내는 것이라면, 비선형 회귀는 곡선을 찾아내는 것이다. 오늘은 비선형 회귀를 MATLAB으로 어떻게 구현하는지 알아보자.
어떤 한 동네의 원룸 월세가 아래와 같다고 가정해보자.

데이터를 보기 쉽게 그래프로 나타내면 다음과 같다.

우리가 하고 싶은 것은 data fitting을 해서 이 데이터를 가장 잘 설명할 수 있는 곡선, 즉 함수를 찾는 것이다. 이 데이터를 잘 설명할 수 있을 것 같은 함수의 형태는 아래와 같다.

눈치 빠른 분들은 이미 알아차리셨겠지만 일종의 시그모이드(sigmoid) 함수다. nonlinear fitting을 위해서는 이러한 함수를 잘 찾아주는 것이 중요하다. 데이터의 분포를 이차 함수로 잘 fitting 해낼 수 있을 것 같으면 이차 함수로, 3차 함수가 적당할 것 같으면 3차 함수로, 로그 함수가 적당할 것 같으면 로그 함수로 해주는 것이다.
이제 관건은 최적의 파라미터들 b1, b2, b3를 찾는 것이다. 그 작업을 nlinfit 함수가 해준다. nlinfit은 nonlinear fitting의 약자다. 먼저 b1, b2, b3에 대한 초기 값을 설정해준다. 제대로 된 b1, b2, b3를 찾기 위해서는 가장 실제와 비슷할 만한 값으로 설정해주는 것이 좋다. 그래서 나는 b1 = (월세의 최댓값) - (월세의 최소값), b2 = (평수의 평균값), b3 = (월세의 최솟값)으로 초기설정해줬다. 그 다음에 nlinfit 함수를 실행하면 이 데이터 분포에 가장 적합하다고 생각하는 b1, b2, b3를 알려준다. 이제 b1은 초기값 25에서 25.1082로, b2는 초기값 7.8792에서 8.2202로, b3는 초기값 19에서 19.2907로 조정되었다. 이 조정된 파라미터들을 대입해서 함수의 그래프를 그려보면 아래와 같이 굵은 선으로 표현된다. 데이터를 적절히 fitting 했음을 확인할 수 있다.
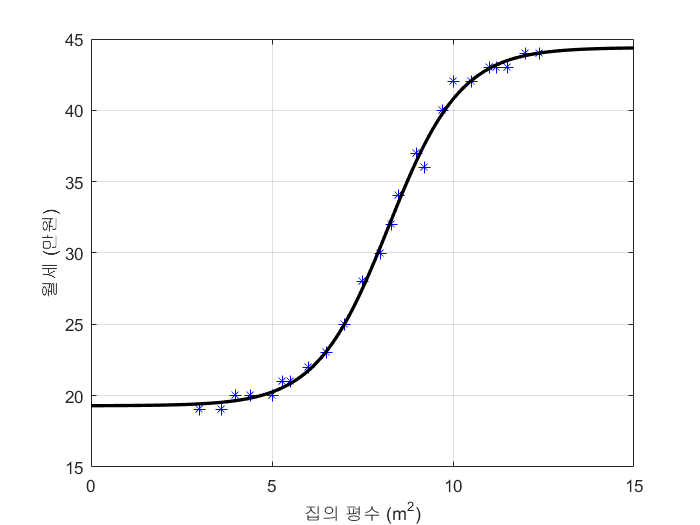
이제 nlpredci 함수(nonlinear regression prediction confidence intervals)를 이용하면 임의의 평수에 대한 월세를 예측할 수 있다. 평수가 3.5, 7.8, 13.2일 때의 월세를 예측해보자. 사실상 파라미터가 조정된 함수에 x값들을 대입하는 과정이라고 보면 된다.

빨간 십자가로 표시된 부분이 평수 3.5, 7.8, 13.2에 대한 월세들을 알려주는 지점들이다. 3.5평의 집은 19.5125만원, 7.8평은 29.2454만원, 13.2평은 44.2275만원의 월세가 예상된다.
이 전체 과정에 대한 MATLAB 코드는 다음과 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
clc, clear, close all
x = [3; 3.6; 4; 4.4; 5; 5.3; 5.5; 6; 6.5; 7; 7.5; 8; 8.3; 8.5; 9; 9.2; 9.7; 10; 10.5; 11; 11.2; 11.5; 12; 12.4]; % 집의 평수
y = [19; 19; 20; 20; 20; 21; 21; 22; 23; 25; 28; 30; 32; 34; 37; 36; 40; 42; 42; 43; 43; 43; 44; 44]; % 월세
plot(x, y, 'b*');
xlabel('집의 평수 (m^2)');
ylabel('월세 (만원)');
grid on
modelfun = @(b, x)(b(1)./(1+exp(-x+b(2)))+b(3));
b = [max(y)-min(y); mean(x); min(y)];
[beta, R, J] = nlinfit(x, y, modelfun, b); % beta에 b의 업데이트된 값이 저장된다.
t = 0:0.01:15;
[ypred1, delta1] = nlpredci(modelfun, t, beta, R, 'Jacobian', J);
hold on;
plot(t, ypred1, 'Color', 'black', 'LineWidth', 2);
test_x = [3.5; 7.8; 13.2]; % 월세를 예측하고 싶은 집의 평수들
[test_ypred, delta] = nlpredci(modelfun, test_x, beta, R, 'Jacobian', J); % test_ypred에 예측된 월세가 저장된다.
plot(test_x, test_ypred, 'r+', 'MarkerSize', 10, 'LineWidth', 5);
|
cs |
코드를 한 줄씩 분석해보면 그다지 어렵지 않을 것입니다. 혹시 궁금점 또는 잘못된 점이 있다면 댓글로 남겨주세요.^^
'Dev > matlab' 카테고리의 다른 글
| [MATLAB] inline 함수 활용하기 (0) | 2019.12.16 |
|---|---|
| [MATLAB] 그레이스케일 이미지를 RGB 이미지로 멋드러지게 표현하기, ind2rgb 함수 (0) | 2019.11.29 |
| [MATLAB] 반올림, 올림, 내림, round, ceil, floor 함수 (0) | 2019.11.09 |
| [MATLAB] 숫자가 아닌 것 찾기, isnan 함수 (0) | 2019.11.08 |
| [MATLAB] 로그스케일 그래프 그리기, semilogy, semilogx, loglog 함수 (0) | 2019.10.23 |
| [MATLAB] 엑셀 파일의 내용 불러오기, xlsread 함수 (0) | 2019.10.23 |
| [MATLAB] 숫자열에 숫자가 아닌 것(NaN)이 포함되어 있을 때 평균내기, mean 함수 응용 (0) | 2019.10.19 |
| [MATLAB] 적분하기, integral 함수 (7) | 2019.10.17 |