지금까지 정보량, 엔트로피, 결합 엔트로피, 조건부 엔트로피를 설명해왔습니다. 오늘은 상호정보량을 다룰 차례입니다.
두 개의 확률변수 사이의 상호정보량(mutual information)은 하나의 확률변수가 다른 하나의 확률변수에 대해 제공하는 정보의 양을 의미합니다. 이것을 I(X; Y)로 표현합니다. I(X; Y)는 다음과 같이 계산할 수 있습니다.
$ \begin{align*} I(X; Y) &= \sum _{x,y}p(x,y){log}_2\frac{p(x,y)}{p(x)p(y)}\\ &= \sum _{x,y}p(x,y){log}_2p(x,y) - \sum _{x,y}p(x,y){log}_2p(x) - \sum _{x,y}p(x,y){log}_2p(y)\\ &= -H(X, Y) + H(X) + H(Y)\\ &= H(X) - H(X|Y)\\ &= H(Y) - H(Y|X)\\ &= I(Y; X) \end{align*} $
이 식의 전개에서 알 수 있듯이 X가 Y에 대해 제공하는 정보량과 Y가 X에 대해 제공하는 정보량은 같습니다. I(X; Y) = I(Y; X)라는 뜻입니다. 따라서 상호 정보량을 두 확률변수가 공유하는 엔트로피라고 해석해도 됩니다.
그리고 만약 두 확률변수가 독립이라면, 즉 p(x, y) = p(x)p(y)이라면, 상호정보량은 0이 됩니다. 위 식의 첫번째 행에 대입해보면 알 수 있죠.
확률변수 X, Y에 대한 결합확률분포표가 다음과 같을 때 상호 정보량을 계산해보도록 하겠습니다.
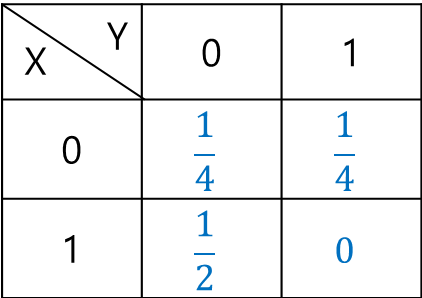
저는 I(X; Y) = H(X) + H(Y) - H(X, Y)를 이용해서 계산해보겠습니다. 먼저 H(X)부터 구하면, 다음과 같습니다.
$ H(X) = \frac{1}{2}{log}_22 + \frac{1}{2}{log}_22 = 1 $
그리고 H(Y)는 다음과 같습니다.
$ H(Y) = \frac{3}{4}{log}_2\frac{4}{3} + \frac{1}{4}{log}_24 = 0.8113 $
또한 H(X, Y)는 다음과 같습니다.
$ H(X, Y) = \frac{1}{4}{log}_24 + \frac{1}{4}{log}_24 + \frac{1}{2}{log}_22 = 1.5 $
따라서, I(X; Y) = I(Y; X) = 1 + 0.8113 - 1.5 = 0.3113 입니다.
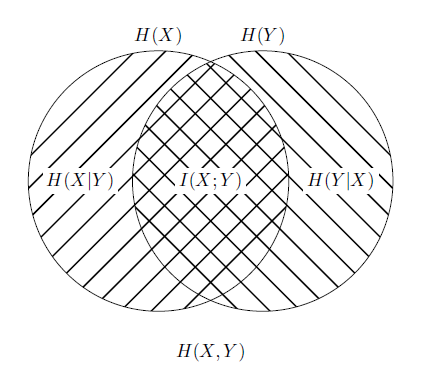
마지막으로 좀 더 직관적인 이해를 위해, 엔트로피, 조건부 엔트로피, 결합 엔트로피, 상호 정보량을 벤 다이어그램으로 나타내면 다음과 같은 형태가 됩니다. X의 엔트로피와 Y의 엔트로피의 교집합이 바로 X, Y의 상호 정보량에 해당하는 것이죠. 여기서도 알 수 있는 것이 만약 두 확률변수가 독립이라면 교집합이 존재하지 않으니 상호 정보량이 0이 된다는 것입니다.
나름 이해되는 대로 정리해봤는데, 여전히 쉽진 않네요.^^;
<참고자료>
[1] https://arxiv.org/abs/1304.2333, Felix Effenberger, "A primer on information theory, with applications to neuroscience"
'Research > 확률, 통계' 카테고리의 다른 글
| 이산 확률 분포 정리(균일분포, 이항분포, 포아송분포) (1) | 2022.10.13 |
|---|---|
| 가우시안(정규) 분포와 라플라스 분포의 차이 (14) | 2020.06.12 |
| 직관적으로 쉽게 이해하는 베이즈 정리 (수식은 저리 치워) (2) | 2020.04.15 |
| [정보이론] 결합(joint) 엔트로피와 조건부(conditional) 엔트로피 (0) | 2019.10.25 |
| [정보이론] 정보량과 엔트로피의 의미 (2) | 2019.10.25 |
| kullback-leibler divergence(KL 발산)의 간략한 설명 (14) | 2019.09.09 |
| 자료를 대표하는 숫자, 대표값: 평균, 중앙값, 최빈값 (0) | 2019.06.03 |
| 모평균의 신뢰구간 추정하기 (31) | 2019.05.16 |