선형보간법(linear interpolation)에 대해서는 잘 설명된 자료가 많지만, 삼차보간법(cubic interpolation)에 대해서는 읽을 만한 괜찮은 자료를 찾기가 쉽지 않습니다. 아마도 삼차보간법에 대해 글을 쓰신 분들도 완벽하게 원리를 이해하고 쓴 것이 아닌 것 같습니다. 아인슈타인이 이렇게 말했죠. "만약 당신이 무엇인가를 쉽게 설명할 수 없다면, 그것을 제대로 이해한 것이 아니다." 이 글이 삼차보간법과 쌍삼차보간법을 이해하는데 있어 여러분들께 통찰력을 제공하길 바랍니다.
우선 보간법(interpolation)이라는 것이 무엇인지 간략히 설명하고 넘어가겠습니다. 보간법이란 알려진 값을 가진 두 점 사이 어느 지점의 값이 얼마일지를 추정하는 기법을 의미합니다. 아래 그림을 보시면 a와 b사이에 위치한 x의 값, 즉 f(x)가 무엇인지를 추정하는 것이 바로 보간법입니다.

선형보간법(linear interpolation)
보간법에는 여러가지 접근법이 있는데, 그중 비교적 간단한 선형보간법은 두 점 사이에 직선을 그립니다. 그리고 그 선을 이용해서 f(x)를 추정합니다. 다음 그림과 같이 말이죠.

두 점의 좌표를 알면 1차 함수식을 만들 수 있죠? y = mx + n에 두 좌표값을 대입시키면 그 1차 함수식을 찾아낼 수 있습니다. 그러면 결과적으로 다음과 같은 함수식이 도출됩니다.
$y = \frac{f(a)-f(b)}{a-b}x+\frac{af(b)-bf(a)}{a-b}$
식이 복잡해보인다고 겁먹지 마세요.^^ 어려운 것 아닙니다. 중요한 것은 일차함수식을 찾아냈다는 것입니다. 일차함수식을 찾아냈기 때문에, a와 b 사이의 어떤 점 x의 함수값, 즉 f(x)도 그 식에 대입함으로써 알아낼 수 있습니다. 이것이 바로 선형보간법의 핵심입니다. 기억해야할 것은 선형보간법에서는 값을 추정할 때 두 개의 점을 참조했다는 점입니다.
삼차보간법(cubic interpolation)
보간법에는 다양한 접근법이 존재한다고 했습니다. 그 중 하나가 방금 설명한 선형보간법이었습니다. 선형보간법은 1차 함수를 활용한 것이었죠? 이제 설명드릴 삼차보간법은 3차(cubic) 함수를 활용합니다. 삼차보간법은 우리가 알고 있는 두 점 a, b가 삼차함수 그래프 위에 있다고 가정합니다. 다음과 같이 말이죠.
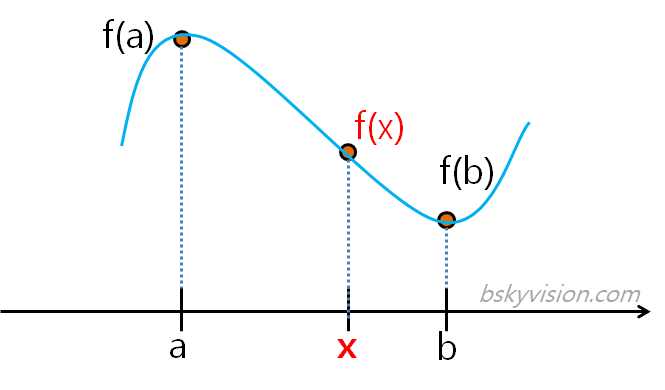
이렇게 3차 함수를 이용해서 미지의 값을 추정하면 일차 함수를 통해 찾는 것보다 훨씬 더 부드러운 결과를 만들어낼 수 있습니다. 직선이 아닌 곡선을 이용하기 때문이죠. 문제는 이 3차 함수 $f(x) = mx^3 + nx^2 + jx + k$를 알아내야 한다는 점입니다. m, n, j, k를 찾아내야 한다는 뜻이죠.
문제를 간단하게 만들기 위해서 $a = 0$, $b =1$이라고 가정하고 출발하겠습니다. 그리고 $f(0) = y_0$, $f(1) = y_1$로 놓겠습니다.
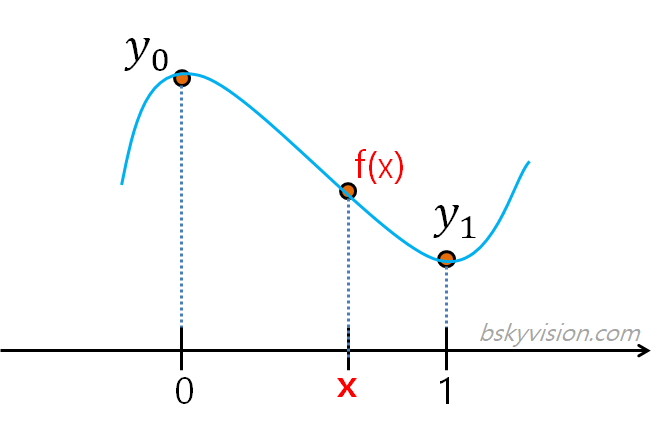
자, 그럼 함께 m, n, j, k를 계산해봅시다. 우선 k는 쉽게 구할 수 있겠네요. f(x)에 0을 대입하면, f(0) = k가 나옵니다. k는 이미 알고 있는 값인 $y_0$입니다.
$k = y_0$ ...(1)
이제 네 개 중에 하나 구했습니다. 이번엔 f(x)에 1을 대입해볼까요? 그러면 다음과 같은 식을 얻을 수 있습니다.
$f(1) = m + n + j + k = y_1$
여기서 k는 아까 $y_0$임을 알았으니 대입해서 정리하면 미지수가 세 개인 방정식을 하나 얻게 됩니다.
$m + n + j = y_1 - y_0$ ...(2)
미지수가 세 개인 방정식이 세 개 있으면 연립해서 그 미지수들을 모두 구할 수 있죠? 그것을 위해 f(x)를 x에 대해 미분한 후에 0과 1을 각각 대입시켜보겠습니다. 그러면 방정식을 두 개 얻을 수 있겠죠? 우선 f(x)를 미분하면, 다음과 같이 됩니다.
$f'(x) = 3mx^2 + 2nx + j$
그 다음에 0과 1을 각각 대입하면,
$f'(0) = j$ ...(3)
$f'(1) = 3m + 2n + j$ ...(4)
과 같은 방정식들이 도출됩니다. 이제 세 개의 방정식이 생겼으니 연립해서 풀면 됩니다. 그런데 연립방정식을 풀기 위해서는 먼저 f'(0)과 f'(1)을 알아야합니다. 우리가 다루는 데이터가 연속적(continuous)인 경우라면 미분해서 값을 넣어주면 되지만, 이산적(discrete)인 경우에는 다음과 같이 미분값들을 구할 수 있습니다. 기울기(미분값)는 y의 증가량을 x의 증가량으로 나눠준 것임을 중학생 때 배웠던 것 같습니다.
$f'(0) = \frac{y_1 - y_{-1}}{2}$
$f'(1) = \frac{y_2 - y_0}{2}$
따라서 우리는 $(0, y_0)$, $(1, y_1)$말고도, 추가적으로 두 점 $(-1, y_{-1}), (2, y_2)$도 참조해야합니다. 그래서 삼차보간법은 이웃한 두 개를 참조하는 선형보간법과 달리 네 개의 점을 참조합니다.

이제 f'(0)과 f'(1)을 방정식 (3), (4)에 각각 대입하겠습니다.
$j = \frac{y_1 - y_{-1}}{2}$ ...(3)
$3m + 2n + j = \frac{y_2 - y_0}{2}$ ...(4)
이 과정에서 j도 알게 되었네요. 방정식 (2)와 (4)에 j를 대입해서 나머지 m, n을 구해봅시다. 먼저 j를 대입하면 방정식 (2), (4)가 다음과 같이 정리됩니다.
$m + n = \frac{y_{-1} - 2y_0 + y_1}{2}$ ...(2)-1
$3m + 2n = \frac{y_{-1} - y_0 - y_1 + y_2}{2}$ ...(4)-1
이 친구들을 연립해서 풀면, m과 n을 구할 수 있습니다. 구했더니 이렇게 나오네요.
$m = - \frac{y_{-1}}{2} + \frac{3}{2}y_0 - \frac{3}{2}y_1 + \frac{y_2}{2}$ ...(2)-2
$n = y_{-1} - \frac{5}{2}y_0 + 2y_1 - \frac{y_2}{2}$ ...(4)-2
드디어 우리가 알아야할 m, n, j, k를 모두 찾아냈습니다. $f(x) = mx^3 + nx^2 + jx + k$를 찾아낸 것이죠. 0과 1사이에 존재하는 어떤 x의 함수값, f(x)도 우리는 이제 이 함수를 이용해서 추정할 수 있습니다. 이것이 바로 삼차보간법입니다. 다시 한번 말하지만 수식은 중요하지 않습니다. 이렇게 전개된다는 것 정도만 알고 계시면 됩니다.
쌍선형보간법(bilinear interpolation)과 쌍삼차보간법(bicubic interpolation)
선형보간법을 2차원으로 확장시킨 것이 바로 쌍선형보간법이고, 삼차보간법을 2차원으로 확장시킨 것이 쌍삼차보간법입니다. 2차원으로 확장시킨 것 외에 원리상 달라진 것은 없습니다. 쌍선형보간법은 이웃한 4(=2x2)개의 점을 참조하고, 쌍삼차보간법은 16(=4x4)개의 점을 참조합니다.
이제 마무리 인사를 드릴 시간이네요. 끝까지 읽고 생각하시느라 수고하셨습니다. 블로그를 운영하면서 알게된 진리는 "힘들게 쓴 글은 독자들이 알아준다"는 것입니다. 이 글도 꽤 어렵게 썼습니다. 따라서 이 글도 누군가 알아주실 것을 기대하며 글을 마칩니다.^^ 항상 질문과 지적은 환영입니다. 댓글로 남겨주시면 빠르게 답변드리도록 하겠습니다.
b스카이비전의 추천글
☞ 초해상화(Super-resolution)란? 저화질 영상을 고화질로 바꿔주는 기술
☞ [MATLAB] 이미지 크기 조정하기, imresize 함수
☞ [python] opencv-python 패키지 유용한 함수 10개 정리
<참고자료>
[1] https://dsp.stackexchange.com/questions/18265/bicubic-interpolation, stackexchange, "bicubic interpolation"
[2] https://darkpgmr.tistory.com/117, 다크프로그래머, "선형 보간법"
'Research > 컴퓨터비전, 영상처리' 카테고리의 다른 글
| 머리 자세 추정(head pose estimation)에서 pitch, roll, yaw angle이란? (1) | 2020.07.31 |
|---|---|
| 동적 텍스처(dynamic texture) 분류란? (0) | 2020.06.29 |
| [IQA] 완벽한 블라인드 품질 평가 방법을 제안한 NIQE (1) | 2020.06.05 |
| [IQA] 이미지품질평가 분야의 셀럽, BRISQUE (9) | 2020.06.03 |
| 지각(perception)과 인지(cognition)의 차이 이해하기 (25) | 2020.05.26 |
| 최소식별차(just-noticeable-difference)와 영상압축 (2) | 2020.05.25 |
| 사람들이 자연 풍광 사진을 실내 및 도시 사진보다 선호하는 이유는? (2) | 2020.05.20 |
| 등방성(isotropic) 이미지와 이방성(anisotropic) 이미지란? (0) | 2020.05.19 |