분류 모델의 평가할 때 널리 사용되는 것 중에 confusion matrix가 있습니다. confusion matrix를 한국어로 오차 행렬, 혼돈 행렬, 혼동 행렬이라고 번역하기도 합니다. confusion matrix가 중요한 이유 중 하나는 이것 하나만 있으면, 분류 모델의 예측 성능을 평가할 때 주로 사용되는 정확도(accuracy), 정밀도(precision), 재현율(recall), F1 점수 등을 모두 구할 수 있기 때문입니다.
scikit-learn의 confusion matrix
더 깊은 설명으로 들어가기 전에 우선 파이썬 scikit-learn 라이브러리를 활용하여 confusion matrix를 구해보겠습니다. 클래스가 True, False 또는 1, 0 또는 양성, 음성과 같이 두 개 밖에 없는 이진 분류의 경우 confusion matrix는 다음과 같이 구해집니다. 예시를 위해 테스트셋의 라벨과 예측된 라벨 정보 리스트를 임의로 만들었습니다.
from sklearn import metrics
y_test = [1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0] # 실제 클래스
y_pred = [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0] # 예측된 클래스
confusion_matrix = metrics.confusion_matrix(y_test, y_pred)
print(confusion_matrix)
위 코드를 실행하면, 다음과 같은 confusion matrix가 터미널에 출력됩니다.

각 위치의 숫자가 의미하는 바는 다음과 같습니다. 우선 5부터 살펴보겠습니다.

같은 행에 있는 3의 의미는 다음과 같습니다.
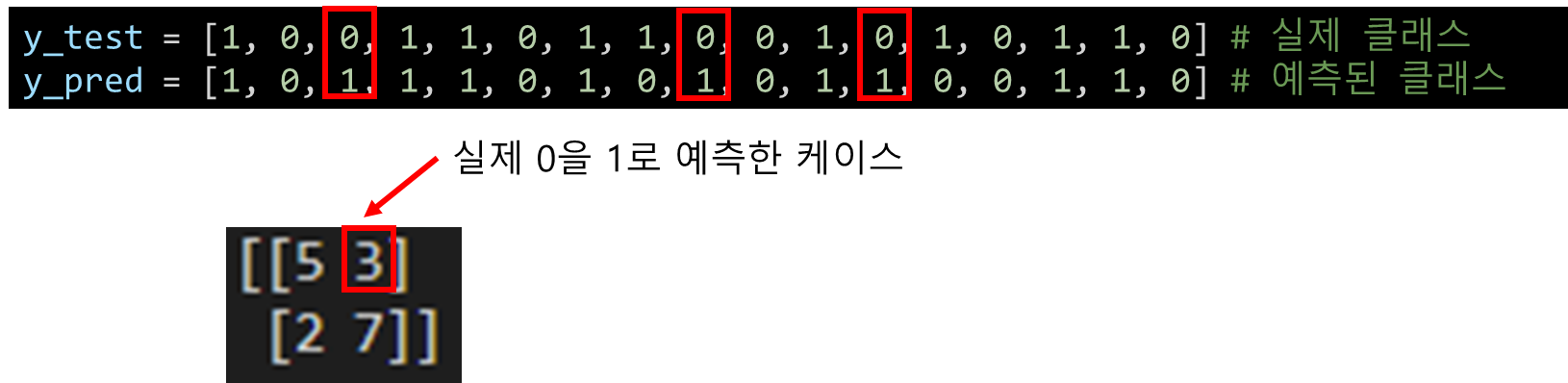
2번째 행의 2는 다음과 같은 의미를 갖습니다.
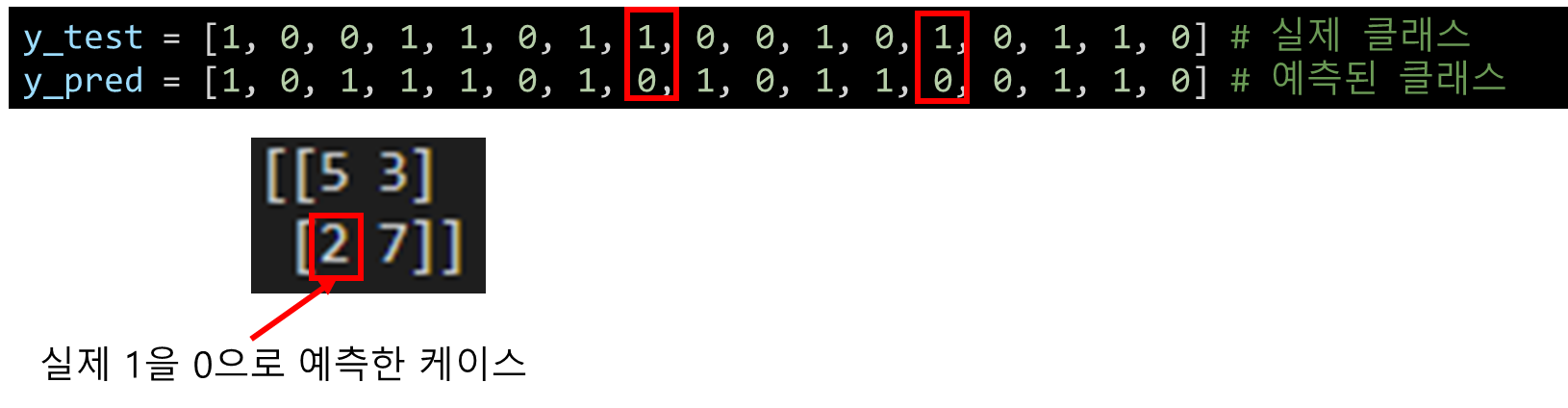
2번째 행의 7의 의미는 다음과 같습니다.

정리하자면, 다음과 같습니다. scikit-learn으로 구한 confusion matrix에서 행은 실제값, 열은 예측값을 나타냅니다.

정확도 (accuracy)
서두에서 confusion matrix가 있으면 정확도, 정밀도, 재현율, F1 점수를 모두 구할 수 있다고 했습니다. 하나씩 구하는 방법과 그 의미를 살펴보겠습니다. 우선 정확도는 다음과 같은 공식으로 구할 수 있습니다.
정확도 = (TP + TN) / (TP + TN + EP + FN)
정확도 = (5 + 7) / (5 + 3 + 2 + 7) = 12 / 17 = 0.71
전체 샘플 중에 제대로 클래스를 예측한 샘플의 비율이 바로 정확도입니다.
정밀도 (precision)
정밀도 = TP / (TP + FP)
정밀도 = 7 / (7 + 3) = 0.70
정밀도는 양성으로 예측한 것 중에 실제 양성의 비율을 나타냅니다.
재현율 (recall)
재현율 = TP / (TP + FN)
재현율 = 7 / (7 + 2) = 0.78
재현율은 실제 양성 중에서 양성으로 예측된 것의 비율을 나타냅니다.
그런데 정확도로 예측력을 평가하면 되지, 왜 정밀도, 재현율 같은 것들이 필요한 거지? 의문을 던지실 수 있습니다. 자, 그렇다면 아래와 같은 경우를 생각해보겠습니다.
어떤 사람이 암에 걸렸는지 안 걸렸는지를 판별해야 하는 의료 기기가 있다고 가정해보겠습니다. 이 의료 기기는 암에 걸린 사람은 무조건 암에 걸렸다고 양성 판정을 해줘야 합니다(TP). 그래야 환자가 빠르게 치료를 받을 수 있기 때문입니다. 설령 암에 안 걸린 사람을 암에 걸렸다고 잘못 판정을 하더라도 말입니다(FP). 이 경우에는 나중에 정밀 검사 후 암이 아닌 사실을 발견하고 가슴을 쓸어내리겠죠. 반면, 암에 걸렸는데 암에 안 걸렸다고 잘못 예측하는 경우(FN)는 거의 없어야 합니다. 따라서, 이러한 의료 기기는 재현율이 높아야 합니다. TP가 많고 FN이 적으면 재현율은 높아집니다.
의료기기를 만드는 개발자가 재현율을 높여야 이 의료기기가 잘 팔릴 거라 생각해서 모든 케이스에 양성 판정을 내리는 말도 안 되는 야매 기기를 만들었다고 가정해보겠습니다. 이 경우에 재현율은 1이 됩니다. 양성은 당연히 양성으로 예측될 것(TP)이고요, 양성을 음성으로 잘못 예측한 경우(FN)가 0이기 때문입니다.
항상 양성으로 예측하는 경우, 재현율 = TP / (TP + 0) = 1
하지만, 이러한 기기의 정밀도는 매우 떨어집니다. 정밀도는 양성으로 예측한 것 중에 실제 양성의 비율이니 음성인데 양성으로 예측한 경우(FP)가 터무니 없게 많다면 정밀도는 낮아질 수밖에 없습니다.
항상 양성으로 예측하는 경우, 정밀도 = TP / (TP + 큰 FP) = 작음
F1 점수
보통 재현율이 비정상적으로 높은 분류 모델의 정밀도는 낮을 수 밖에 없습니다. 반대로 정밀도가 과하게 높은 경우에는 재현율이 낮을 수 밖에 없습니다. 따라서, 재현율과 정밀도가 동시에 높아야 진정 예측력이 좋은 분류 모델이라고 할 수 있기 때문에 이 둘의 조화평균으로 F1 점수라는 것을 구합니다.
F1 = (2*정밀도*재현율) / (정밀도 + 재현율)
F1 = (2*0.7*0.78) / (0.7 * 0.78) = 0.74
F1 점수가 높아야 진정 예측력이 좋다고 보는 것입니다.
scikit-learn으로 정확도, 정밀도, 재현율, F1 점수 구하는 코드
참고로 scikit-learn에서 정확도, 정밀도, 재현율, F1 점수를 구할 때 사용하는 메소드는 각각 다음과 같습니다.
1) 정확도: metrics.accuracy_score()
2) 정밀도: metrics.precision_score()
3) 재현율: metrics.recall_score()
4) f1 점수: metrics.f1_score()
accuracy = metrics.accuracy_score(y_test, y_pred)
print("정확도:", accuracy)
precision = metrics.precision_score(y_test, y_pred)
print("정밀도:", precision)
recall = metrics.recall_score(y_test, y_pred)
print("재현율:", recall)
f1 = metrics.f1_score(y_test, y_pred)
print("f1 점수:", f1)
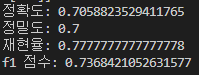
위에서 저희가 직접 구한 것과 동일한 결과가 나오는 것을 확인하실 수 있습니다.
언제 정확도를 사용하고, 언제 F1 점수를 사용해야 하는가?
그런데 아직도 의문이 풀리지 않는 부분이 있으실 것입니다. 정확도라는 아주 간단하고 이해하기 쉬운 평가 방법이 있는데 왜 굳이 F1 점수가 왜 필요하지라는 생각을 하시는 분들이 있을 것 같습니다. 다음과 같은 경우를 생각하시면 이해가 될 것입니다. 테스트셋의 라벨이 [1, 1, 1, 0, 0, 0, 0, 0, 0, 0]으로 0이 1에 비해 비교적 많은 상황이라고 가정하겠습니다. 이 테스트셋에 대해 예측된 라벨이 [1, 0, 0, 0, 0, 0, 0, 0, 0, 0] 이라고 하면, 정확도는 8/10 = 0.8입니다.
정확도 = 8 / 10 = 0.8
10개 중에 2개 틀렸으니까요. 사실 그냥 모든 케이스를 0으로 예측해버렸더라도 정확도는 0.7이나 나왔을 것입니다. 이렇게 데이터의 클래스가 한쪽에 쏠려 있는 상황에서는 정확도로 예측력을 평가하는 것은 적절치 못합니다.
반면, 정밀도와 재현율을 구한 후 F1 점수를 구해보면, 다음과 같이 F1 점수는 0.496으로 상당히 낮게 나오는 것을 알 수 있습니다.
정밀도 = TP / (TP + FP) = 1 / (1 + 0) = 1
재현율 = TP / (TP + FN) = 1 / (1 + 2) = 0.33
F1 점수 = (2*정밀도*재현율) / (정밀도 + 재현율) = (2*1*0.33) / (1 + 0.33) = 0.496
이렇게 클래스 분포가 균형적이지 않고, 양성(1)을 음성(0)으로 잘못 예측하는 것이 치명적인 경우(예를 들어, 암 판정)에는 정확도보다는 F1 점수로 모델의 예측력을 평가하는 것이 더 좋습니다. 이 모델에는 0.8(정확도)이라는 점수보다 0.496(F1 점수)이라는 점수가 더 잘 어울리지 않나요?
정리하며
오늘은 분류 모델의 성능을 평가하는데 사용되는 confusion matrix, 정확도, 정밀도, 재현율, F1 점수에 대해서 알아봤습니다. confusion matrix만 구하면, 나머지는 쉽게 구할 수 있다는 것도 확인했습니다. 또한 어떤 상황에서 정확도를 사용해야하는지, F1 점수를 사용해야 하는지도 살펴봤습니다. 저희가 실생활에서 마주하는 데이터는 대부분 클래스 분포가 불균형(imbalanced)하기 때문에 분류 모델의 성능을 평가할 때는 정확도보다는 F1 점수를 조금 더 많이 활용한다는 점을 말씀드리며 글을 맺도록 하겠습니다.
관련 글
- 이진 분류기 성능 평가방법 AUC(area under the ROC curve)의 이해
참고 자료
[2] 안드레아스 뮐러, 세라 가이도 지음, "파이썬 라이브러리를 활용한 머신러닝", 한빛미디어(2017)
[3] medium, Purva Huilgol, "Accuracy vs. F1-score"
[4] statology, "F1 Score vs. Accuracy: Which Should You Use?"
'Dev > python' 카테고리의 다른 글
| [python] yaml 파일 파이썬에서 읽기 (0) | 2022.10.28 |
|---|---|
| [python] 문자열 대소문자 변환하기 (upper, lower, isupper, islower) (0) | 2022.10.25 |
| [python] 0으로 채워진 1차원, 2차원 리스트(배열) 만들기 (0) | 2022.10.11 |
| [python] 리스트에서 최대값, 최소값의 인덱스 구하기 (0) | 2022.10.09 |
| [python] 딕셔너리에서 value가 가장 큰 key 알아내는 방법 (0) | 2022.10.07 |
| [python] 10진수를 2진수, 8진수, 16진수로 변환하는 방법 (4) | 2022.10.03 |
| [pandas] 컬럼 값이 특정 조건에 부합하는 행들의 특정 컬럼 값 수정하기 (0) | 2022.10.02 |
| [pandas] 데이터프레임 행 또는 컬럼 삭제하기, drop() 메소드 (0) | 2022.10.01 |