
지난 강의:
[bskyvision의 선형대수학, 제0강] 동기부여: 선형대수학 F 받았던 학생이 선형대수학을 이용해서 SCI 논문을 쓰다
[bskyvision의 선형대수학, 제1강] 벡터와 선형결합
[bskyvision의 선형대수학, 제2강] 점곱과 길이
지난 시간까지 우리는 벡터에 대해 이야기해왔습니다. 오늘은 드디어 행렬(matrix)이 등장할 차례입니다. 준비되신 줄로 믿고, 시작하겠습니다.
행렬(matrix)
세 벡터 u, v, w의 선형 결합을 우리는 다음과 같이 썼습니다.

그런데 행렬을 이용하면 다음과 같이 세 벡터 u, v, w를 행렬의 열로 각각 넣어주고, c, d, e 스칼라들을 요소로 하는 벡터를 곱해주는 형태로 쓸 수도 있습니다. 그것을 고등학교 때 배운 방식으로 계산해보면 위에서 선형 결합해준 결과와 동일하게 나옵니다.

고등학교 때 행렬과 벡터를 곱해주는 방식을 대학 수준으로 고상하게 표현하자면, 행렬의 각 행벡터들과 벡터를 점곱해준 것입니다.
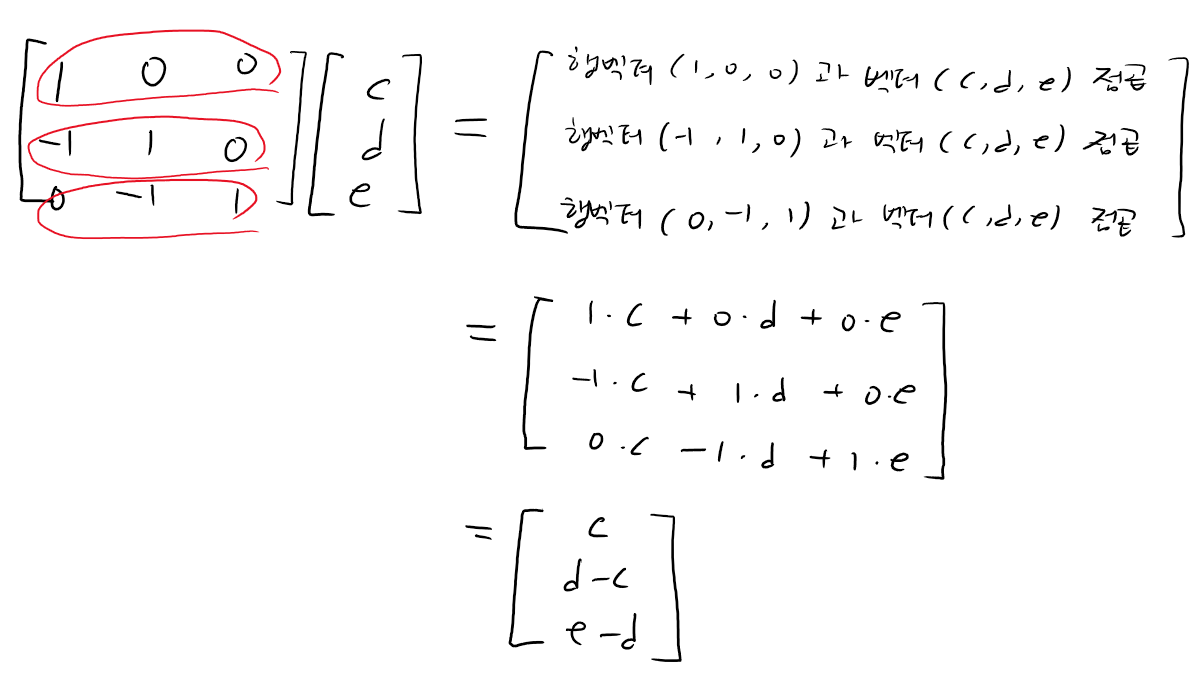
이제 우리는 벡터들의 선형 결합을 행렬과 벡터의 곱의 형태로 나타낼 수 있게 된 것입니다. 만약 u, v, w 열벡터들로 이뤄진 행렬을 A라고 하고, 스칼라들을 c, d, e 대신에 x1, x2, x3로 쓰고 그것을 요소로 삼은 벡터를 x라고 하고, 선형 결합의 결과 벡터를 b라고 한다면 다음과 같이 표기할 수 있겠죠.
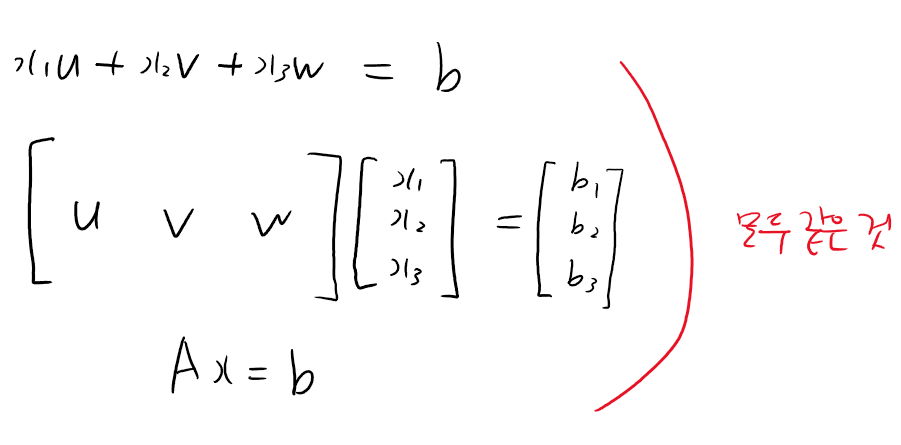
벡터들의 선형 결합을 행렬과 벡터의 곱으로 나타낼 수 있다는 것, 매우 중요한 포인트니 꼭 기억해두세요.
일차 방정식들
A가 3x3 행렬인 경우에 Ax = b는 3개의 1차 방정식으로 나타낼 수 있습니다. 행렬 A의 각 행벡터들과 벡터 x를 점곱해준 결과죠.

이 친구들을 연립해서 풀면, 해 x1, x2, x3가 각각 무엇인지 알아낼 수 있습니다. 즉, 벡터 x가 무엇인지 알아낼 수 있습니다.
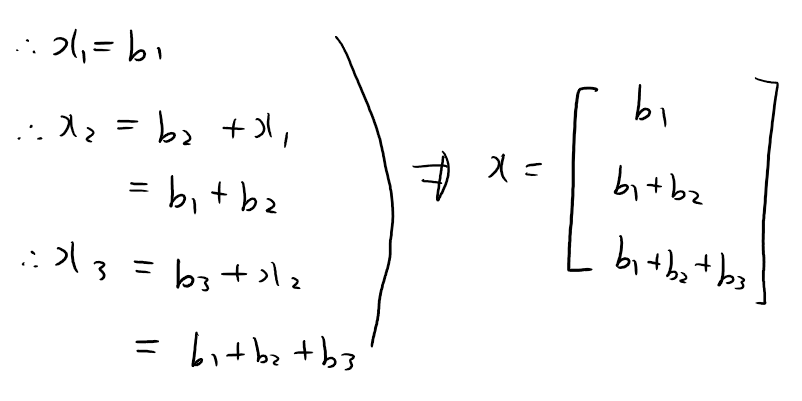
만약 벡터 b가
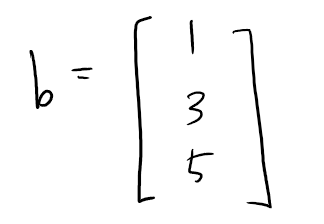
이라면, 벡터 x는
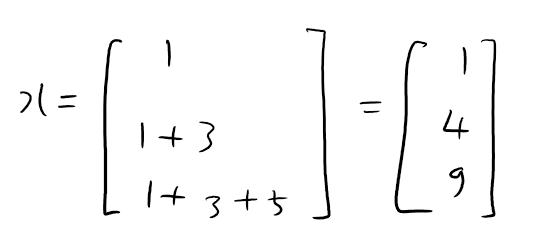
이 됩니다. 만약 b가 영벡터

라면, 벡터 x는
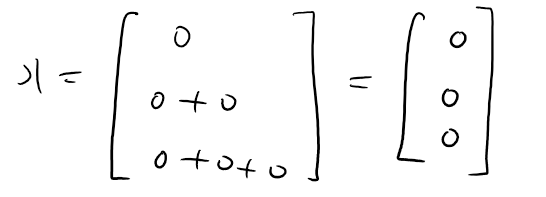
이 됩니다. 여기서 중요한 것은 영벡터 b를 만들 수 있는 벡터 x는 영벡터밖에 없다는 점입니다. 여기서 소개해드린 행렬 A의 경우에는 그렇습니다. 이러한 특성을 가진 행렬을 가역(invertible) 행렬이라고 부릅니다. 가역 행렬은 역행렬(inverse matrix)을 갖는 행렬이라는 뜻입니다. 역행렬을 갖는 행렬의 경우에는 단 하나의 해를 가집니다.
역행렬(inverse matrix)
우리는 방금 위에서 Ax=b로부터 벡터 x를 구했었습니다. 그러면 이번엔 어떤 행렬을 벡터 b에 곱해줘야 벡터 x가 나올지에 대해서 생각해보겠습니다.

우선 벡터 x가 3 x 1 이므로, 물음표에 해당하는 행렬은 3 x 3 행렬이 되어야 할 것입니다. [3 x 3] [3 x 1] = [3 x 1]
그리고 물음표 행렬의 첫번째 행 벡터는 뭐가 되어야 벡터 b = (b1, b2, b3)를 점곱해줬을 때 b1이 될까요?
바로 벡터 (1, 0, 0)입니다.
그리고 두번째 행 벡터는 뭐가 되어야 벡터 b를 점곱해줬을 때 b1 + b2가 될까요?
바로 벡터 (1, 1, 0)입니다.
마지막으로 세번째 행 벡터는 (1, 1, 1)이 되어야 벡터 b를 점곱해줬을 때 b1 + b2 + b3가 됩니다.
따라서, 다음과 같은 행렬을 벡터 b에 곱해주면 벡터 x가 나옵니다.

이 물음표 행렬이 바로 행렬 A의 역행렬입니다.
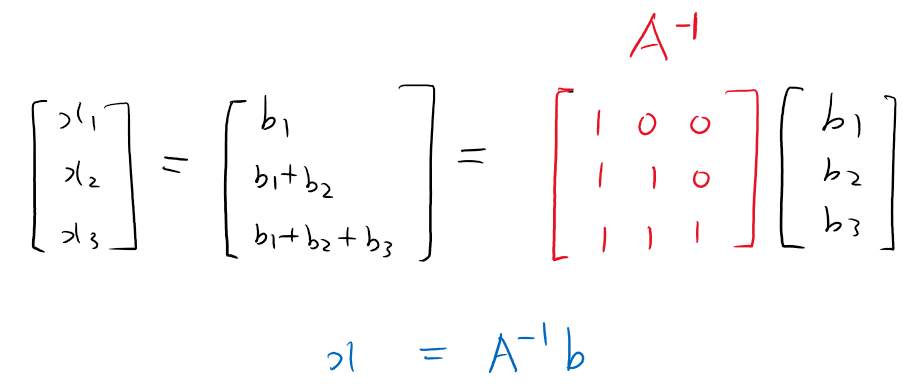
따라서 A가 가역 행렬인 경우 Ax=b는 다음과 같이 풀 수 있습니다. Ax=b는 A의 역행렬만 찾으면(찾을 수 있다면), 풀리는 것이죠.
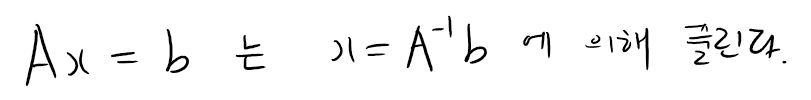
특이 행렬(singular matrix)
좀 전에도 말씀드렸지만, 모든 행렬이 역행렬을 갖는 것은 아닙니다. 그렇지 않은 경우들도 있습니다. 하나의 예를 들어보겠습니다.
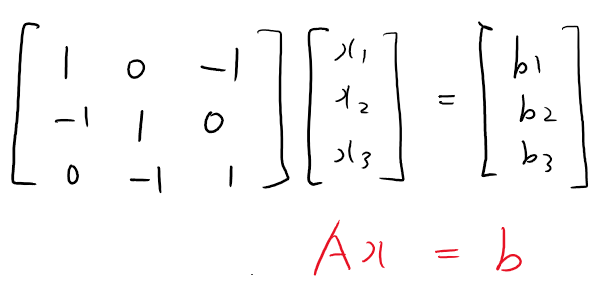
여기에서 세 개의 1차 방정식을 뽑아내면 각각 다음과 같습니다.
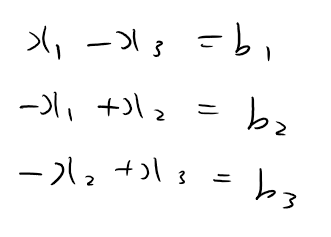
이 친구는 뭔가 연립해서 푸려고 하면 잘 안 풀립니다. 뭔가 하나의 변수가 소거가 되어야 풀리는데, 어떻게 해도 하나만은 소거가 안됩니다. 왜냐하면 좌변을 모두 더해보면 0이 되고, 우변을 모두 더해보면 b1+b2+b3가 되기 때문입니다.

이 Ax=b가 성립하려면, 지극히 예외적으로 b1=b2=b3=0이고, x1=x2=x3이어야 합니다. x1=x2=x3=c 로 어떠한 수도 될 수 있기 때문에, 이 경우에는 해가 무수히 많게 됩니다.

b = (0, 0, 0)이 아니면, 이 Ax=b는 풀 수가 없습니다. 다른 말로, 해가 없습니다. 이렇게 해가 무수히 많거나 해가 없는 행렬은 역행렬을 갖지 않습니다. 이런 행렬들을 특이 행렬(singular matrix)이라고 부릅니다. 역행렬을 갖지 않으므로 비가역 행렬이라고 부를 수도 있습니다.
독립(independence)과 종속(dependence)
위에서 예를 든 가역 행렬의 경우, 행렬을 구성하는 열 벡터들이 서로 선형 독립(independent)입니다. 하나의 열 벡터에 어떤 스칼라를 곱한다고, 다른 열 벡터가 될 수 없습니다. 또한 두 개의 열 벡터를 선형 결합한다고 해서, 나머지 열 벡터를 만들어낼 수도 없습니다.
그런데, 위에서 예로 든 특이 행렬의 경우는, 행렬을 구성하는 열 벡터들이 종속적(dependent)입니다. w가 u와 v의 선형 결합으로 만들어집니다.
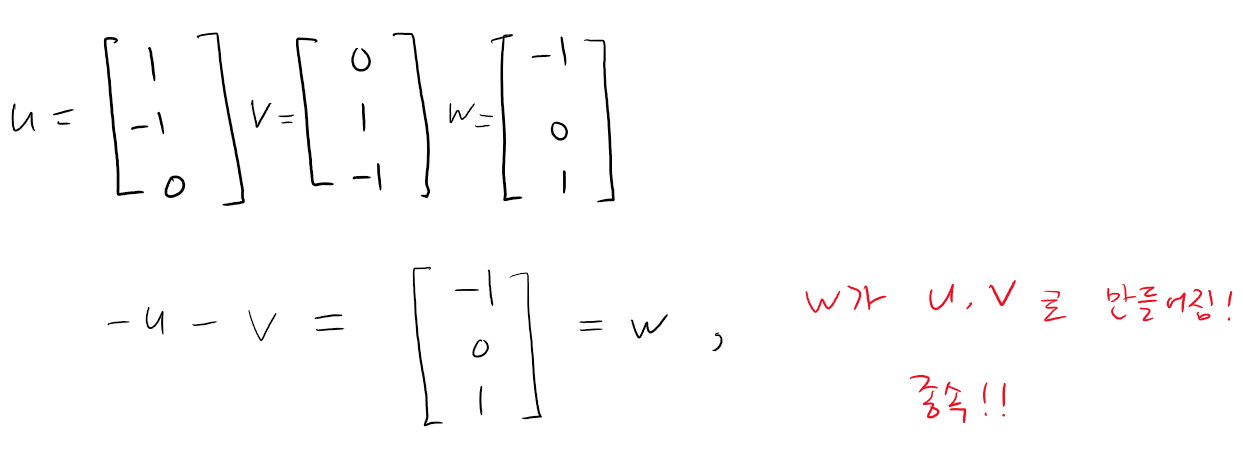
이 경우에는 u, v, w을 어떻게 선형 결합하더라도 하나의 평면을 벗어나지 못합니다.
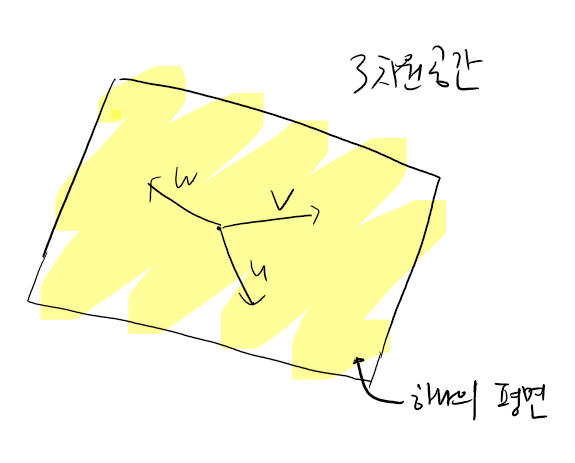
정리하자면, 3x3 가역 행렬들을 구성하고 있는 열 벡터들의 선형 결합은 3차원 공간의 어디에도 미칠 수 있습니다. 반면, 비가역 행렬들을 구성하고 있는 열벡터들의 선형 결합은 3차원 공간의 하나의 평면에 국한되거나 하나의 선에 국한되어 버립니다. 하나의 선에 국한되는 케이스는 벡터 v, w가 u의 어떠한 스칼라를 곱한 것과 같은 경우입니다. 예를 들어, v = 2u, w = -0.5u 이런 경우라면 세 벡터를 어떻게 선형 결합해도 하나의 선을 벗어날 수 없습니다.
가역 행렬은 독립적인 열 벡터들을 갖고, 특이 행렬은 종속적인 열 벡터들을 갖습니다. 이 독립과 종속의 개념, 제1강에서도 설명했지만 정말 중요하니 꼭 기억하고 넘어가셔야 합니다.
제3강 끝
오늘은 개인적으로 글을 쓰면서 쉽게 설명하기가 쉽지 않다는 생각이 들었습니다. 헤메고 계시진 않을까 걱정이 되네요. 그래도 부디 잘 따라와주셨길 바래봅니다.ㅎㅎ 막히는 부분이 있으면, 질문을 해주세요.
만약 어떤 책을 참고해서 공부하고 계시다면, 꼭 그 책의 연습문제를 많이 풀어보시길 권해드립니다. 솔루션이 없는 책이라고 하더라도, 푸는 과정에서 정말 많은 것들을 이해하게 됩니다. 연습문제는 되도록 많이 풀어보세요! 이런저런 예제를 통해 다양하게 접근해봐야, 선형대수학의 진수를 제대로 이해할 수 있습니다. 이론적으로 이해가 잘 안 될 때는 무조건 연습문제를 많이 풀어보는 것이 좋습니다. 하나씩 푸는 과정에서 이론적인 내용을 자연스럽게 습득하게 되니까요.
이 글의 내용 및 그림들은 함부로 가져가지 말아주세요.
제가 꽤 많은 시간을 투자해서 작성하고 그린 것이니 이곳에서만 봐주시길 바랍니다.
이 글을 어딘가에 링크를 거는 것은 괜찮습니다.
'Research > 선형대수학' 카테고리의 다른 글
| [bskyvision의 선형대수학, 제6강] 행렬을 이용한 소거법 (14) | 2021.03.01 |
|---|---|
| [bskyvision의 선형대수학, 제5강] 소거법 (elimination) (10) | 2021.02.17 |
| [bskyvision의 선형대수학, 제4강] row picture와 column picture (6) | 2021.02.08 |
| [bskyvision의 선형대수학, 제2강] 점곱과 길이 (0) | 2021.01.25 |
| [bskyvision의 선형대수학, 제1강] 벡터와 선형결합 (6) | 2021.01.18 |
| [bskyvision의 선형대수학, 제0강] 동기부여: 선형대수학 F 받았던 학생이 선형대수학을 이용해서 SCI 논문을 쓰다 (8) | 2021.01.13 |
| [선형대수학] 놈(norm)이란 무엇인가? (13) | 2020.06.25 |
| [선형대수학] 고유값과 고유벡터의 물리적 의미는? (4) | 2019.12.23 |