**작년(2021년)에 이어 올해(2022년)도 한국대학생스포츠협의회(KUSF)에서 주최하는 스포츠 데이터 분석 교육 프로그램에서 강사로 참여하게 되었습니다. 그래서 기존에 세이버메트릭스 관련해서 작성했던 글들을 리뉴얼하는 작업을 하고 있습니다.
야구는 기본적으로 상대방보다 더 많은 득점을 기록하는 팀이 이깁니다. 득점을 많이 하고 실점을 적게 하는 팀은 이길 확률이 높습니다. 따라서, 한 시즌의 득점과 실점의 비율과 승률 사이에는 강한 상관관계가 있습니다.
승률 = 승 / (승 + 패)
....(공식1)
득실점비율 = 기대승률(WPCT) = 피타고리언 승률 = 득점^2 / (득점^2 + 실점^2)
....(공식2)
아래 산점도(scatter plot)는 MLB의 1954년부터 2019년까지의 팀 득실점 비율과 승률 사이의 상관관계를 보여줍니다. 여기서 각 포인트는 어떤 해, 어떤 팀의 득실점비율과 승률을 보여줍니다.

우선 육안으로 보더라도 굉장히 상관성이 큰 것으로 보입니다. 데이터의 분포가 하나의 직선으로 쉽게 모델링이 될 것 같으면(데이터의 분포가 하나의 직선으로 표현이 된다면), 상관성이 큰 것입니다.
어느 정도 상관성이 있는지 하나의 수치로 나타내기 위해 득실점비율과 승률 사이의 상관계수를 구해보겠습니다.
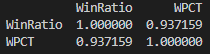
피어슨 상관계수를 구했더니 무려 0.9372입니다. 득실점비율과 승률 사이에는 매우 강한 상관관계가 있다는 것입니다. 이 말인즉슨 득점, 실점의 비율만 알면 승률을 거의 예측할 수 있다는 것입니다.
참고로 위 산점도와 상관계수는 다음과 같은 파이썬 코드로 구현했습니다.
import sqlite3
import pandas as pd
import matplotlib.pyplot as plt
with sqlite3.connect("lahmansbaseballdb.sqlite") as con:
cur = con.cursor()
cur.execute('''select W, L, R, RA from teams where yearID >= 1954;''')
data = cur.fetchall()
df_data = pd.DataFrame(data, columns=['W', 'L', 'R', 'RA'])
df_data['WinRatio'] = df_data['W'] / (df_data['W'] + df_data['L'])
df_data['WPCT'] = df_data['R']**2 / (df_data['R']**2 + df_data['RA']**2)
print(df_data)
df_data.plot(x='WinRatio', y='WPCT', kind='scatter')
plt.show()
print(df_data[['WinRatio', 'WPCT']].corr())
저는 기대승률 공식에서 지수를 2로 했는데, 1.83으로 하면 좀 더 정확하다고 합니다. 그래서 MLB 관련 유명 야구 통계 사이트인 베이스볼 레퍼런스는 2가 아닌 1.83을 사용한다고 합니다.
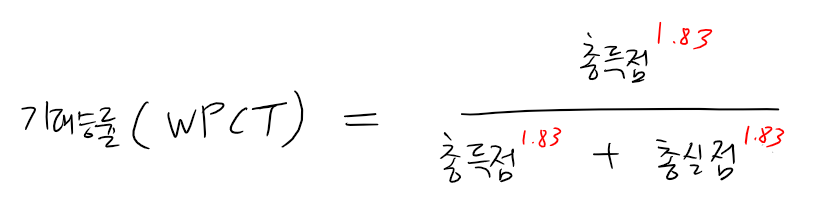
위 기대승률은 비단 야구에만 사용될 수 있는 것이 아닙니다. NBA, NFL등에서도 사용되는데, NBA에서는 지수를 14에서 17 사이로 설정해주고, NFL에서는 2.4로 설정한다고 합니다[1].
기대 승률을 어떻게 활용하는 것이 좋을까?
이 기대 승률을 어떻게 활용할 수 있을까요? 어떤 팀이 시즌 절반을 마친 상황에서 승률이 6할이었다고 가정해보겠습니다. 그런데, 기대 승률을 구해봤더니 5할이었다면, 이 팀은 현재까지 운이 좋은 편이었다고 볼 수 있습니다. 기대 승률이 5할이라는 뜻은 총득점수와 총실점수가 완전히 같았다는 것입니다. 1/(1 + 1) = 0.5
그런 상황에서 6할의 승률을 거둔 것이니 비교적 운이 좋았다고 볼 수 있는 것이죠. 질 때는 크게 지고, 이길 때는 간신히 이긴 경우가 많았을 것 같습니다. 하지만, 남은 경기들에서도 지금과 같이 1에 가까운 득실점 비율을 기록한다면, 남은 경기에서는 5할 근처의 승률을 거둘 가능성이 큽니다. 지금처럼 운이 계속 좋지 않은 이상 말이죠.
이미 치룬 절반의 시즌에서는 6할의 승률을 기록했고, 남은 절반 시즌의 기대 승률은 5할이므로 55% (0.5*0.6 + 0.5*0.5) 정도의 승률로 시즌을 마무리할 가능성이 있습니다.
그러면 기대 승률을 가지고 올 시즌(2022) KBO 정규시즌 최종 순위를 한 번 예측해볼까요? 아래 기록은 2022년 5월 28일 00:41 기준 KBO 리그 순위입니다. SSG가 높은 승률로 1위를 달리고 있죠.

그리고 아래 표는 각 팀의 득점, 실점, 현재승률, 기대승률(WPCT), 이번 시즌 최종 예상 승률, 이번 시즌 최종 예상 순위를 담은 표입니다.
| 팀명 | 득점 | 실점 | 현재승률 | 기대승률 | 최종 승률 예측 | 최종 순위 예측 |
| SSG | 228 | 160 | 0.717 | 0.670 | (1/3)*0.717 + (2/3)*0.670 = 0.6857 | 1 |
| 키움 | 210 | 188 | 0.583 | 0.555 | (1/3)*0.583 + (2/3)*0.555 = 0.5643 | 3 |
| LG | 222 | 195 | 0.563 | 0.564 | (1/3)*0.563 + (2/3)*0.564 = 0.5637 | 4 |
| KIA | 238 | 206 | 0.553 | 0.572 | (1/3)*0.553 + (2/3)*0.572 = 0.5657 | 2 |
| 두산 | 211 | 197 | 0.511 | 0.534 | (1/3)*0.511 + (2/3)*0.534 = 0.5263 | 5 |
| 삼성 | 197 | 199 | 0.489 | 0.495 | (1/3)*0.489 + (2/3)*0.495 = 0.4930 | 6 |
| 롯데 | 185 | 205 | 0.447 | 0.449 | (1/3)*0.447 + (2/3)*0.449 = 0.4483 | 8 |
| KT | 178 | 185 | 0.478 | 0.481 | (1/3)*0.478 + (2/3)*0.481 = 0.4800 | 7 |
| 한화 | 183 | 265 | 0.313 | 0.323 | (1/3)*0.313 + (2/3)*0.323 = 0.3197 | 10 |
| NC | 183 | 235 | 0.354 | 0.377 | (1/3)*0.354 + (2/3)*0.377 = 0.3693 | 9 |
우선 기대승률은 위 공식2를 이용해서 구했습니다. 그리고 최종 승률 예측은 현재 시즌이 약 1/3정도 지났기 때문에 현재 승률에 1/3을 곱한 것과 남은 시즌에 해당하는 2/3을 기대승률에 곱한 것을 서로 더해서 구했습니다. 통계에서 기대값(expected value)을 구하는 것과 유사한 방식을 사용했습니다.
그랬더니 최종 1위는 SSG가 차지할 것으로 예측되었고, 현재 4위를 달리고 있는 KIA가 2위로 올라설 것으로 예측되었습니다. 또한 현재 9위인 한화는 10위로 내려앉을 것으로 예상됩니다. 이 순위가 어느 정도 맞았는 지는 시즌이 끝난 후에 한 번 확인해봅시다^^
관련 글
1. [세이버메트릭스] 레먼 데이터베이스에서 류현진 선수 MLB 기록 살펴보기(sqlite3)
2. [세이버메트릭스] 타율이 높은 팀 vs OPS가 높은 팀, 누가 이길까?
3. [python+pandas] 튜플의 리스트를 데이터프레임으로 만들기
참고자료
[1] 벤저민 바우머, 앤드루 짐발리스트 지음, "세이버메트릭스 레볼루션"
[2] namu.wiki/w/%ED%94%BC%ED%83%80%EA%B3%A0%EB%A6%AC%EC%95%88%20%EC%8A%B9%EB%A5%A0, 나무위키, "피타고리안 승률"
(이 글은 2022-05-30에 마지막으로 수정되었습니다)
'Research > 야구' 카테고리의 다른 글
| [세이버메트릭스] 타자의 타율, OPS, 삼진비율, 볼넷비율 중 어떤 것을 가장 신뢰할 수 있을까? (12) | 2021.03.09 |
|---|---|
| [세이버메트릭스] 타율, 출루율, OPS, RC 중 무엇이 가장 득점 생산과 연관 있을까? (2) | 2021.03.06 |
| [세이버메트릭스] MLB에서 2019까지 1000안타 이상 친 선수 중, 홈런을 2루타보다 더 많이 쳐낸 선수는? (sqlite3) (12) | 2021.03.05 |
| [세이버메트릭스] 작년 KBO에서는 평균 연봉이 더 높은 구단이 더 잘했을까? (2019년, 2020년 분석) (6) | 2021.03.04 |
| [세이버메트릭스] 선구안이 좋은 선수를 알아볼 수 있는 볼넷삼진비(BB/K) (5) | 2021.03.03 |
| [세이버메트릭스] 상대 투수를 지치게 만드는 선수들, 타석당 투구수 (P/PA) (4) | 2021.03.02 |
| [세이버메트릭스] 레먼 데이터베이스에서 류현진 선수 MLB 기록 살펴보기(sqlite3) (2) | 2021.03.02 |
| [세이버메트릭스] 타자의 파워를 평가하는 장타율과 isop의 차이는? (2) | 2021.02.26 |