지난 시간에 파이썬에 대해 선형 회귀를 실행하는 코드에 대해 살펴봤습니다. 오늘은 지난 시간에 예고한 것처럼 선형 회귀를 업그레이드한 것인 릿지 회귀에 대해 다루도록 하겠습니다. 선형 회귀에 대해 익숙치 않은 분들은 오늘 이 글을 보시기 전에 아래 두 포스팅을 보고 오시길 추천드립니다.
선형 회귀(linear regression) 그리고 라쏘(Lasso)
[파이썬] 선형 회귀(linear regression)
데이터의 특성이 단 하나일 경우에는 선형 회귀나 릿지 회귀나 다를 것이 없습니다. 똑같은 성능을 보입니다. 그러나 특성이 다수일 경우에는 릿지 회귀가 좀 더 잘 작동할 가능성이 큽니다. 릿지 회귀는 선형 회귀와 달리 모델의 복잡도를 조정할 수 있기 때문입니다. 복잡도를 조정할 수 있다는 말은 사용자가 설정 가능한 파라미터가 있다는 뜻으로 받아들이셔도 좋습니다.
선형 회귀의 경우 최적의 가중치들을 선택하기 위해서 타깃값과 예측값의 차를 제곱해서 평균낸 것, 즉 평균제곱오차(mean squared error, MSE)를 최소로 만드는 가중치들을 찾습니다.
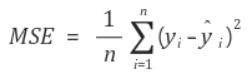
릿지 회귀는 여기에다가 제약 조건을 덧붙입니다. "그 가중치들의 절대값들을 가능한 한 작게 만들어라!" 따라서 릿지 회귀는 다음과 같은 식을 최소로 만드는 가중치들을 찾습니다.
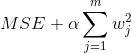
여기서 alpha가 사용자가 설정할 수 있는 파라미터입니다.
그런데 이러한 제약 조건을 붙임으로 얻을 수 있는 효과는 무엇일까요? 만약 alpha 값을 크게 설정해주면 그만큼 가중치들의 절대값들은 작아져야합니다. 그러면 그만큼 기울기가 줄어들겠죠? 기울기가 줄어든다는 말은 특성들이 출력에 미치는 영향력이 줄어든다고 볼 수 있습니다. 즉, 현재 특성들에 덜 의존하겠다는 뜻으로 볼 수 있습니다. 반대로 alpha 값을 작게 설정해주면 가중치들의 절대값들은 조금 커지게 됩니다. 만약 alpha 값을 줄이고 줄여서 0에 가깝게 설정해준다면 사실상 선형 회귀와 동일해지겠죠. alpha가 커지면 커질수록 과소적합이 될 가능성이, alpha가 작으면 작을수록 과대적합이 될 가능성이 커집니다. 따라서 적정한 alpha값을 찾아주는 것은 바로 릿지 회귀를 사용하는 사람의 책임이 됩니다.
자 그럼 이제 릿지 회귀의 성능이 선형 회귀와 비교해서 어떤가를 살펴보겠습니다. 이를 위해 보스턴 주택가격 데이터셋을 활용하겠습니다. 이 데이터셋은 506개의 샘플을 갖고 있고, 각 샘플은 105개의 특성을 갖고 있습니다.
먼저 기존의 선형 회귀의 성능이 어떤지 확인해보도록 하겠습니다. 파이썬 코드는 다음과 같이 작성했습니다.
import mglearn
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.load_extended_boston() # 보스턴 주택가격 데이터셋 불러오기
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) # 데이터셋을 훈련셋과 테스트셋으로 분리
lr = LinearRegression().fit(X_train, y_train) # 선형 회귀 모델 훈련
print("training set score: {:.2f}".format(lr.score(X_train, y_train))) # 훈련셋 결정계수
print("test set score: {:.2f}".format(lr.score(X_test, y_test))) # 테스트셋 결정계수
이 코드를 실행했을 때 터미널에 출력되는 결과입니다.

훈련셋의 점수는 0.95로 상당히 높은 반면에, 테스트셋 점수는 0.61로 좋지 않습니다. 게다가 두 점수의 차이가 크기 때문에 과대적합된 상태입니다. 그렇지만 선형 회귀 모델은 설정가능한 파라미터가 없기 때문에 이 문제를 해결할 방법이 없습니다.
그러면 동일한 데이터셋에서 릿지 회귀는 어떤 성능을 내는지 확인해보겠습니다. 파이썬 코드는 다음과 같이 작성했습니다. 우선 파라미터 alpha를 디폴트 값(alpha = 1)으로 설정했습니다.
import mglearn
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.load_extended_boston() # 보스턴 주택가격 데이터셋 불러오기
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) # 데이터셋을 훈련셋과 테스트셋으로 분리
ridge = Ridge().fit(X_train, y_train) # 릿지 회귀 모델 훈련
print("training set score: {:.2f}".format(ridge.score(X_train, y_train))) # 훈련셋 결정계수
print("test set score: {:.2f}".format(ridge.score(X_test, y_test))) # 테스트셋 결정계수

선형 회귀 모델에 비해 테스트셋 점수가 0.61에서 0.75로 많이 좋아진 것을 알 수 있습니다. 그럼 디폴트값 말고 여러 값을 대입해서 최적의 alpha 값을 찾아보도록 하겠습니다.
alpha = 1보다 큰 값들인 alpha = 2, alpha = 5, alpha = 10으로 설정해보겠습니다. 위 파이썬 코드에서 다음 한 줄만 바꿔주면 됩니다.
ridge = Ridge(alpha=2).fit(X_train, y_train) # 릿지 회귀 모델 훈련



alpha가 1에서 커질수록 오히려 성능이 나빠진것을 확인할 수 있습니다. 따라서 최적의 alpha 값을 찾기 위해서는 alpha값을 줄여가야 합니다. 따라서 alpha를 0.5, 0.1, 0.01과 같은 값으로 설정해보겠습니다.



결과를 통해 알 수 있는 것은 0.5, 0.1로 작아질수록 성능이 좋아지다가 어느 순간부터 다시 나빠집니다. 따라서 alpha = 0.1을 최적의 파라미터값으로 설정해줄 수 있습니다. 물론 더 미세하게 값을 바꿔가면서 최적의 alpha 값을 찾을 수 있겠지만, 이 정도로만 하겠습니다.^^
그럼 최종적으로 선형 회귀와 릿지 회귀 성능을 비교해보겠습니다.

주목해야할 것은 훈련셋 점수가 아니라 테스트셋 점수이므로, 0.77의 결정계수를 가지는 릿지 회귀가 0.61의 선형 회귀보다 보스턴 주택가격 데이터셋에서 우수한 성능을 낸다고 판단할 수 있습니다. (이 결과를 가지고 모든 데이터셋에서 릿지 회귀가 선형 회귀보다 낫다고 단정지을 수는 없습니다.)
다음 시간에는 선형 회귀의 또다른 업그레이드 버전, 라쏘 회귀에 대해 다루도록 하겠습니다. 언제나 질문과 지적은 환영합니다. 댓글 남겨주세요.^^
'Dev > python' 카테고리의 다른 글
| [Anaconda+python] 의상 분류기 만들어서 훈련시키고 테스트하기1(인공신경망) (10) | 2020.02.01 |
|---|---|
| [ubuntu+python] 이미지 속 문자 인식한 것을 음성 파일로 변환해주기 (0) | 2020.01.22 |
| [ubuntu+python] 이미지 속 문자 검출 및 인식하기(OCR) (2) | 2020.01.21 |
| [ubuntu+python] 선형 회귀의 업그레이드 버전2, 라쏘 회귀 (2) | 2020.01.20 |
| [ubuntu+python] pip install과 apt-get install의 차이는? pip와 pip3는 뭐가 다르지? sudo란? (2) | 2020.01.20 |
| [ubuntu+python] 선형 회귀(linear regression) (0) | 2020.01.19 |
| [python] kNN(k-Nearest Neighbors)으로 붓꽃 품종 예측 (18) | 2020.01.18 |
| [ubuntu+python] 웹캠 영상 실시간 물체(객체) 검출 (38) | 2020.01.17 |