오늘은 지난 시간에 선형 회귀의 업그레이드 버전1인 릿지 회귀에 이어 업그레이드 버전2인 라쏘 회귀에 대해 다루도록 하겠습니다. 선형 회귀, 릿지 회귀, 라쏘 회귀에 대해서 이 글을 읽고 이해가 안되신다면 다음 글들을 참고하시면 좀 더 자세한 내용을 확인하실 수 있습니다.
선형 회귀(linear regression)과 라쏘(Lasso)
[파이썬] 선형 회귀(linear regression)
라쏘 회귀는 릿지 회귀와 매우 유사합니다. 모든 것이 동일하고 다른 것은 제약 조건 뿐입니다. 릿지 회귀에서 가중치들의 제곱의 합에 $\alpha$를 곱한 것이 제약 조건이었다면, 라쏘 회귀에서는 가중치들의 절대값의 합에 $\alpha$를 곱한 것이 제약 조건입니다.
릿지 회귀: $\frac{1}{n}\sum_{i=1}^{n}\left ( y_i - \hat{y}_i \right )^2 + \alpha\sum_{j=1}^{m}w_j^2$
라쏘 회귀: $\frac{1}{n}\sum_{i=1}^{n}\left ( y_i - \hat{y}_i \right )^2 + \alpha\sum_{j=1}^{m}|w_j|$
릿지 회귀에 붙은 제약 조건을 전문용어로 L2-norm이라고 불리고, 라쏘 회귀에 붙은 제약 조건은 L1-norm이라고 불립니다. 낯선 용어라 해서 너무 두려워 마시고 그냥 그렇게 부르구나 하고 넘어가셔도 좋습니다.
릿지 회귀의 경우 이전 포스팅에 언급했던 것과 같이 최적의 가중치들은 특성들을 0에 가깝게 만드는 방향으로 진행됩니다. 반면, 라쏘 회귀의 경우 몇몇 특성들이 아예 0이 되어버립니다. 즉, 릿지 회귀의 경우 특성들의 영향력을 낮추는 반면, 라쏘 회귀는 몇몇 특성들을 아예 무력화시켜버립니다. 파라미터 $\alpha$값에 따라 무력화되는 특성들의 갯수가 달라집니다.
자, 그럼 지난 시간에 이용한 보스턴 주택가격 데이터셋에서 라쏘 회귀의 성능을 평가해보도록 하겠습니다. 우선 라쏘 회귀의 파라미터 $\alpha$를 초기값인 1로 놓고 실행해보겠습니다. 파이썬 코드는 다음과 같습니다. 아래 코드를 설치하기 위해서는 numpy, mglearn, matplotlib, scikit-learn 등의 파이썬 패키지가 필요한데, 본인의 컴퓨터에 어떤 패키지가 설치되어있는지 헷갈릴 수 있으니 일단 코드를 실행시켜서 에러난 것을 토대로 하나씩 설치하는 것도 좋은 방법입니다.
import numpy as np
import mglearn
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.load_extended_boston() # 보스턴 주택가격 데이터셋 불러오기
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) # 데이터셋을 훈련셋과 테스트셋으로 분리
lasso = Lasso().fit(X_train, y_train) # 라쏘 회귀 모델 훈련
print("training set score: {:.2f}".format(lasso.score(X_train, y_train))) # 훈련셋 결정계수
print("test set score: {:.2f}".format(lasso.score(X_test, y_test))) # 테스트셋 결정계수
print("the number of the used features: {}".format(np.sum(lasso.coef_ != 0))) # 사용된 특성갯수
usedfeatures = np.nonzero(lasso.coef_ != 0)
print("numbers of the used features: ", usedfeatures[0])# 사용된 특성 번호

훈련셋 점수와 테스트셋 점수가 매우 안좋죠? 그리고 사용된 특성의 갯수를 보니 단 4개입니다. 12번, 79번, 80번, 89번특성만 사용되었습니다. 총 104개의 특성 중에 100개를 제외시켜버린 것입니다. 따라서, 파라미터를 조정해줄 필요가 있습니다. 라쏘 회귀는 적어도 선형 회귀와 비슷한 결과를 낼 수 있는 놈이기 때문입니다. 과소적합인 상황 같으니 모델의 복잡도를 높여주기 위해서, 1보다 작은 $\alpha$ 값들을 시도해보겠습니다. 0.1, 0.01, 0.001을 해보겠습니다. 다음과 같이 $\alpha$ 값을 설정해줄 수 있습니다.
lasso = Lasso(alpha=0.01).fit(X_train, y_train) # 라쏘 회귀 모델 훈련
어떤 값일 때 최적인지 확인해보겠습니다.


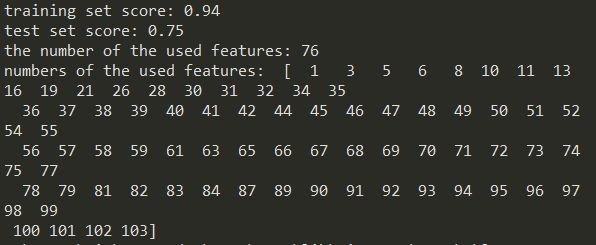
보시다시피 $\alpha$값을 낮추니 성능이 확 좋아졌죠? 그리고 0.01일 때 대략 최적인 것으로 보입니다. 주목할만한 것은 $\alpha$를 낮출수록 사용된 특성의 갯수가 늘어났다는 것입니다. 그만큼 복잡도가 높아진 것이죠. 또한 알파의 값이 0.1, 0.01, 0.001일 때 항상 사용된 특성을 살펴보면 57, 59, 72, 74, 82번 특성들이 있네요.
지난 시간에 해본 릿지 회귀와 비교해서 보스턴 주택가격 데이터셋에서 성능은 거의 비슷한 것으로 보입니다. 데이터셋에 따라 더 좋은 성능을 내는 것을 골라서 사용하시면 되겠습니다.
항상 질문과 지적은 환영입니다. 빠르게 답변드리고 있으니, 댓글 남겨주세요.^^
<참고자료>
[1] 안드레아스 뮐러, 세라 가이도 지음, 박해선 옮김, "파이썬 라이브러리를 활용한 머신러닝", 한빛미디어(2017)
'Dev > python' 카테고리의 다른 글
| [Anaconda+python] 의상 분류기 만들어서 훈련시키고 테스트하기2(컨볼루션 신경망) (12) | 2020.02.05 |
|---|---|
| [Anaconda+python] 의상 분류기 만들어서 훈련시키고 테스트하기1(인공신경망) (10) | 2020.02.01 |
| [ubuntu+python] 이미지 속 문자 인식한 것을 음성 파일로 변환해주기 (0) | 2020.01.22 |
| [ubuntu+python] 이미지 속 문자 검출 및 인식하기(OCR) (2) | 2020.01.21 |
| [ubuntu+python] 선형 회귀의 업그레이드 버전1, 릿지 회귀 (0) | 2020.01.20 |
| [ubuntu+python] pip install과 apt-get install의 차이는? pip와 pip3는 뭐가 다르지? sudo란? (2) | 2020.01.20 |
| [ubuntu+python] 선형 회귀(linear regression) (0) | 2020.01.19 |
| [python] kNN(k-Nearest Neighbors)으로 붓꽃 품종 예측 (18) | 2020.01.18 |