선형회귀는 데이터를 가장 잘 설명해낼 수 있는 직선을 찾아내는 것입니다. 직선은 y = ax + b와 같은 일차함수로 나타낼 수 있는데, 결국 가장 적합한 기울기 a와 x절편 b를 찾아내는 것입니다. (특성이 단 하나인 경우.) 선형회귀에 관한 좀 더 자세한 이론 설명은 이전 글을 참고해주세요.^^
선형 회귀(linear regression) 그리고 라쏘(Lasso)
그럼 간단한 예제를 하나 풀어보겠습니다. 선형 회귀로 해결할 수 있을 것 같은 데이터를 불러와서, 그 중 랜덤하게 75%의 샘플을 선택해서 훈련셋으로 나머지 25%는 테스트셋으로 분리해줍니다. 그 다음에 훈련셋을 이용해서 선형 회귀 모델을 훈련함으로 최적의 a와 b를 구합니다. 그 다음에 y = ax + b(최적의 a와 b를 알게 된 상태)함수에 테스트셋의 각 샘플들의 특성값을 x에 대입시켜줍니다. 그러면 각 샘플의 타겟값에 대한 예측값을 알게 됩니다. 타겟값과 예측값의 상관성을 결정계수를 통해 평가합니다. 결정계수는 1에 가까울수록 예측이 정확하다는 의미를 갖습니다.
이를 실행해주는 코드는 다음과 같습니다. 코드를 실행하기 앞서 scikit-learn, matplotlib, mglearn 라이브러리를 설치해주셔야합니다.^^ 이 부분은 여러분의 검색능력을 믿고 남겨놓겠습니다. "python install 라이브러리명 운영체제명"와 같은 검색어로 찾으시면 쉽게 적당한 것을 찾으실 수 있을 것입니다.
import mglearn
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_wave(n_samples=60) # make data points
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42) # 데이터셋을 훈련셋과 테스트셋으로 분리
plt.plot(X_train, y_train, 'o') # 훈련 데이터 포인트들 그리기
plt.plot(X_test, y_test, '*', color='green') # 테스트 데이터 포인트들 그리기
plt.xlabel("Feature")
plt.ylabel("Target")
lr = LinearRegression().fit(X_train, y_train) # train a linear regressor
print("a: {}".format(lr.coef_)) # 훈련으로 찾아낸 최적의 a
print("b: {}".format(lr.intercept_)) # 훈련으로 찾아낸 최적의 b
y_pred = lr.predict(X_test) # 테스트셋의 데이터들의 타깃값 예측
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.savefig('data points.png') # save plot
plt.show() # display plot
print("training set score: {:.2f}".format(lr.score(X_train, y_train))) # 훈련셋 결정계수
print("test set score: {:.2f}".format(lr.score(X_test, y_test))) # 테스트셋 결정계수

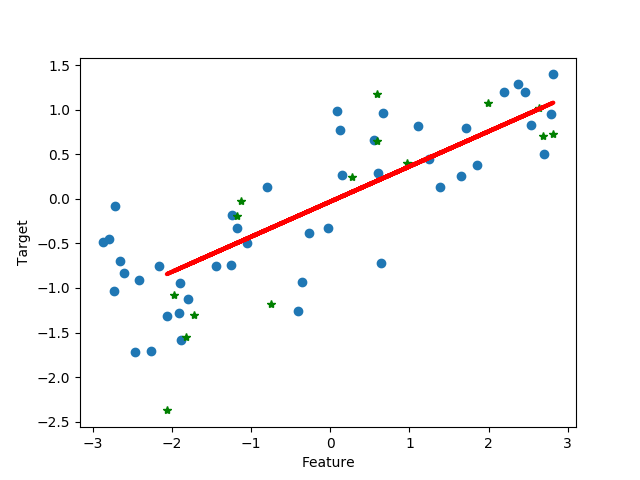
위 코드를 실행했더니, 선형회귀 모델을 훈련시켜서 얻은 a와 b는 다음과 같았습니다.
a = 0.3939, b = -0.0318
즉, 선형회귀 모델은 훈련셋을 이용해서 y = 0.3939x - 0.0318이라는 일차함수를 찾아낸 것입니다. (위 그래프에서 빨간선이 바로 그 일차함수입니다.) 이 일차함수에 훈련셋의 특성값과 테스트셋의 특성값을 각각 대입한 다음에, 결정계수를 구했더니 훈련셋의 결정계수는 0.67이었고, 테스트셋의 결정계수는 0.66이었습니다. 테스트셋의 결정계수가 0.66이므로 성능이 엄청 나쁜 것은 아니지만 그렇다고 좋은 것도 아닙니다. 예측 성능이 충분히 좋진 않다는 뜻입니다. 그러나 훈련셋의 결정계수와 큰 차이가 없는 것은 좋은 일입니다. 훈련셋에 과대적합(overfitting)이 되지 않았고, 오히려 과소적합(underfitting)인 상황이기 때문입니다. 가장 좋은 결과는 테스트셋 점수와 훈련셋 점수가 모두 1에 가깝고, 둘의 차이가 적은 경우입니다.
지금의 경우에는 특성이 단 하나였기 때문에 간단한 선형 회귀도 어느 정도 성능을 냈지만 여러 개의 특성을 갖는 데이터의 경우에는 잘 작동하기 힘듭니다. 다음 시간에는 이에 대한 문제를 집어보고 해결책도 함께 살펴보도록 하겠습니다. 오늘 배운 선형회귀를 조금 업그레이드 시켜보겠습니다.^^ '릿지 회귀'와 '라쏘 회귀'로요.
항상 질문과 지적은 환영입니다. 최대한 빠르게 답변해드리도록 노력하고 있으니 바로바로 댓글 남겨주세요.^^
'Dev > python' 카테고리의 다른 글
| [ubuntu+python] 이미지 속 문자 검출 및 인식하기(OCR) (2) | 2020.01.21 |
|---|---|
| [ubuntu+python] 선형 회귀의 업그레이드 버전2, 라쏘 회귀 (2) | 2020.01.20 |
| [ubuntu+python] 선형 회귀의 업그레이드 버전1, 릿지 회귀 (0) | 2020.01.20 |
| [ubuntu+python] pip install과 apt-get install의 차이는? pip와 pip3는 뭐가 다르지? sudo란? (2) | 2020.01.20 |
| [python] kNN(k-Nearest Neighbors)으로 붓꽃 품종 예측 (18) | 2020.01.18 |
| [ubuntu+python] 웹캠 영상 실시간 물체(객체) 검출 (38) | 2020.01.17 |
| [ubuntu+python] YOLOv3으로 물체(객체) 검출하기 (33) | 2020.01.15 |
| [ubuntu+python] 얼굴 검출 후 성별 인식 (4) | 2020.01.15 |